

Construct a triangle and its medians.Construct a second triangle with the three sides having the lengths of the three medians from your first triangles.Here is GSP sketch.
Find some relationship between the two triangle.Are they cogruent? Similar? Have a same area? Same permeter? Ratio of areas? Ratio of permeters? Here is GSP sketch.
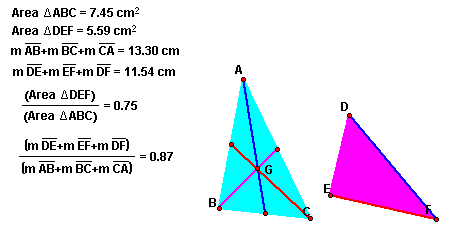
Explore some relationships between two triangles location for various shapes of triangleABC. Then we can discuss the ratio of areas between two triangles is permanence.
Why is the ratio of areas between two triangles 3/4? For explore relationship between two triangles, let's try to construct the second triangle on the original triangle.Here
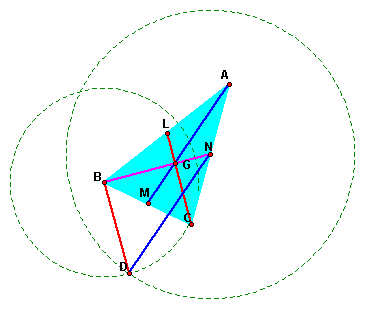 Look at the figure
on right side.The triangle ABC is original .The points L,M,N are
midpoints of sides and G is the centroid. We can construct two
triangles and notice one of the triangle have the sides on a parallel
line with original medians.We should prove this finding fact later.
Any way, this triangle marked BDN.
Look at the figure
on right side.The triangle ABC is original .The points L,M,N are
midpoints of sides and G is the centroid. We can construct two
triangles and notice one of the triangle have the sides on a parallel
line with original medians.We should prove this finding fact later.
Any way, this triangle marked BDN.
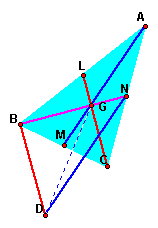 Now focus on the area
of triangle ABC and BDN again. Construct a segment GD.Because
of BD//LC there are same length of bases and hight,TriangleLCB=BDL.
The point of L is midpoint of the side of AB, so the triangle
LCB=BDG=1/2ABC.By the way, the point of G is centroid,so BG:GN=2:1.
Then the heights of the triangle BDG and NDG are same. So the
area of triangle BDG:NDG=2:1,the area of triangle NDG=1/2BDG=1/2*1/2ABC=1/4ABC.
Now focus on the area
of triangle ABC and BDN again. Construct a segment GD.Because
of BD//LC there are same length of bases and hight,TriangleLCB=BDL.
The point of L is midpoint of the side of AB, so the triangle
LCB=BDG=1/2ABC.By the way, the point of G is centroid,so BG:GN=2:1.
Then the heights of the triangle BDG and NDG are same. So the
area of triangle BDG:NDG=2:1,the area of triangle NDG=1/2BDG=1/2*1/2ABC=1/4ABC.
Therefore the area of the triangle DNB=BDG+NDG=1/2ABC+1/4ABC=3/4ABC
When we construct median triangle on the original triangle,we notice there is a median triangle the sides on a parallel with the original medians. If we trancelate two medians parallel with throughing the each sides of the another one, can we connect two trancelate segments on the end ? Is this a median triangle? Let's try to prove the below.
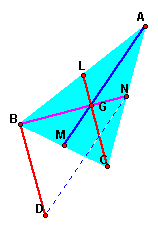 Look at the figure
of left side, the triangle ABC is original.The points of L,M,N
are midpoins and AM,BN and CL are medians.
Look at the figure
of left side, the triangle ABC is original.The points of L,M,N
are midpoins and AM,BN and CL are medians.
When we translate the median LC parallel with troughing the point of B and mark the end of the parallel segment with D, prove the follow.
1. Prove the quadrangle BDCL is parallelism.
2. Prove the length of the segment ND and the median AM are same.
Proof is Here.