

Let's look at the following equation:
The graph of this equation follows:
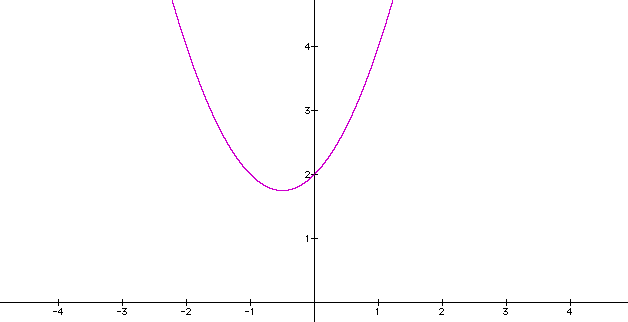
Let's look at what happens when we change (a). I am going to replace (a) with 2, -2, and 0 to see what happens.
Let's look at the graphs of these equations.
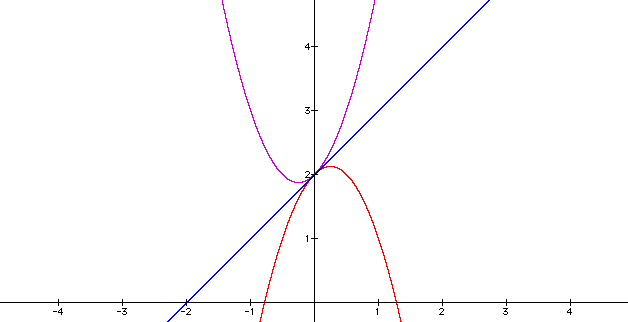
As we can see from these three graphs, there is a common point at (0,2). y=x+2 is the graph of a line through (0,2), and the parabolas and line share a common point at (0,2).
Let's look at the graph when we change (a) to 3, -1, and -3.
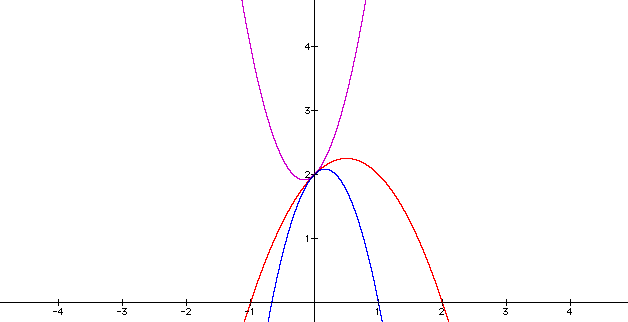
We can see from these three graphs that the parabolas still share a common point at (0, 2).
Let's set (a) to 1 and change (b) to 2, 0, and -1.
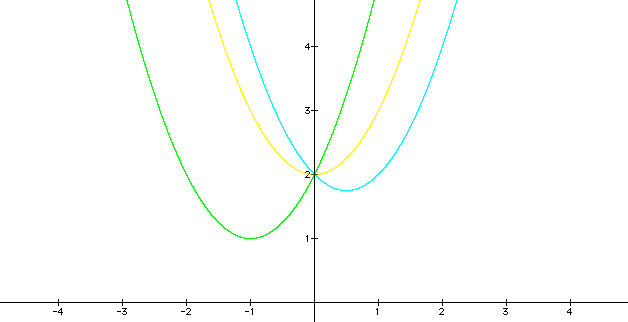
We can see that the graphs still share a common point at (0,2). I must assume that the constant 2 must determine where to place the common point.
Let's set (b) at 1 and change the constant 2 to 1.
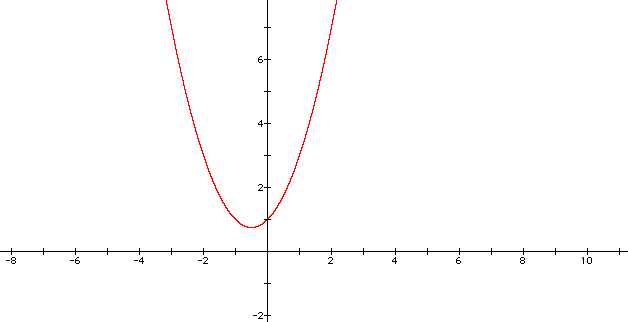
Now we can see that changing the constant moves the graph. Let's see what happens if we change (a) in this equation to -1, 0, and 2. I predict that the graphs will share a common point at (0,1).
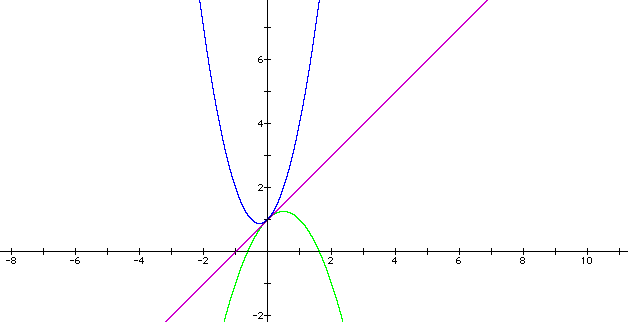
My prediction was correct. All three graphs share a point at (0,1).