

Construct any triangle ABC.
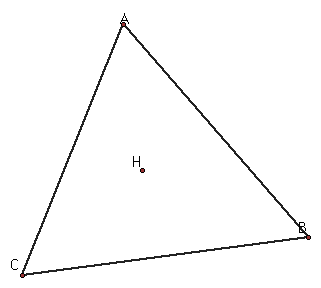
Construct the orthocenter (H) of triangle ABC.
If you need help constructing an orthocenter click here.
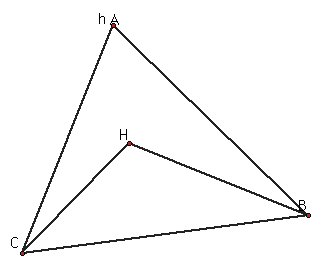
Construct the orthocenter (h) of triangle HBC.
Construct the orthocenter (O) of triangle HAB.
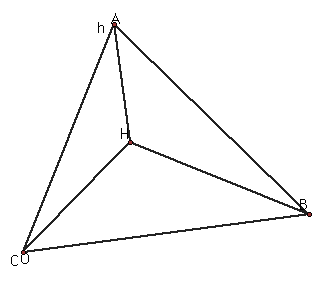
Construct the orthocenter of triangle HAC.
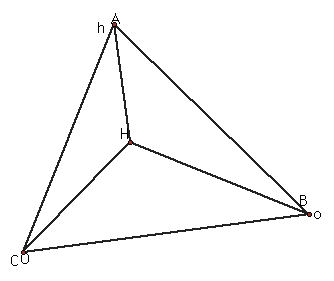
Construct the circumcircles of triangles ABC, HBC, HAB, and HAC.
If you need a reminder about circumcircles click here.
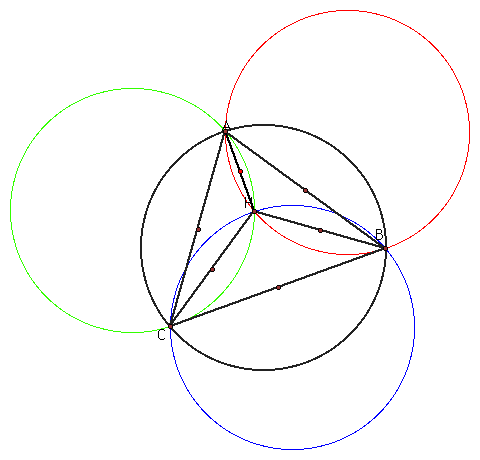
Construct the nine point circles for triangles ABC, HBC, HAC, and HAB.
The nine point circle is the same circle for all four triangles. Why do you think this occured?
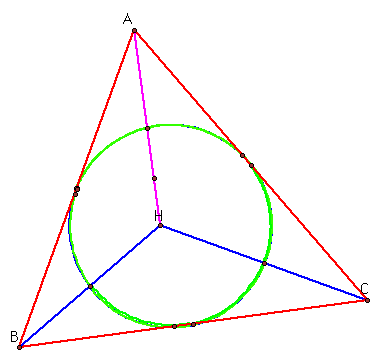
Let's change the shape of the triangle and see what happens.
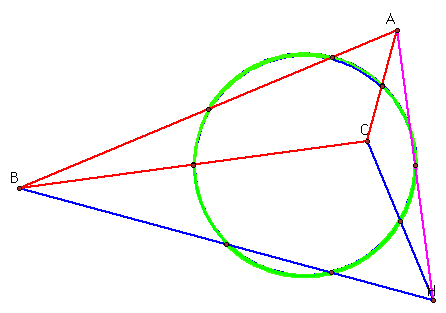
It is still the same circle for all four triangles.
How can we prove this?
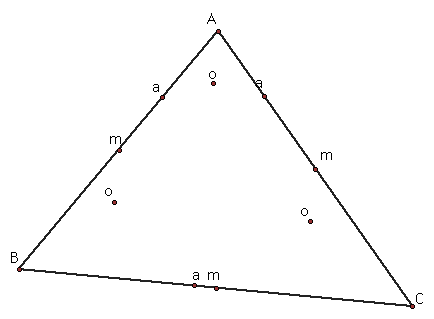
For triangle ABC we found the nine points that form the nine-point circle. We found the midpoints (m), the feet of the altitudes (a), and the midpoints of the segments connecting the vertices to the orthocenter (o).
HBCLet's look at the nine points for the triangle HBC.
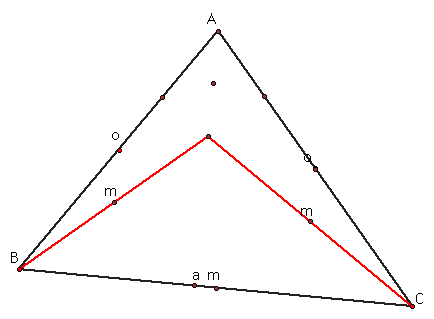
We get the same nine points even though they are not the same midpoints, feet of altitudes, etc.
Let's look at triangle HAB.
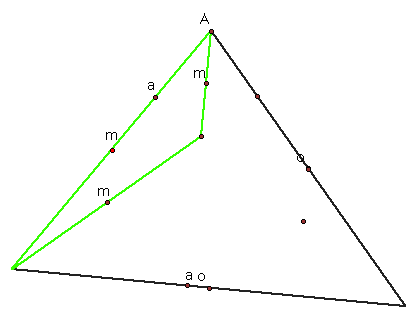
We still get the same nine points, so we can see that all three triangles have the same nine point circle.