
Sinje J. Butler
Write-up 10
Parametric Equations
A parametric curve in the plane is a pair of functions where
the two continuous functions define ordered pairs (x,
y). The extent of the
curve will depend on the range of t.
The following is the graph of the parametric equations
![]()
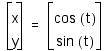
for
![]() .
.
where 6.28 is approximately 2π.
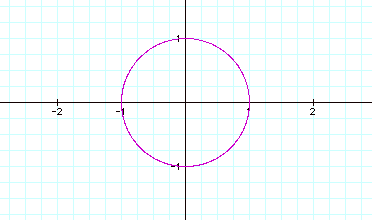
Notice that the unit circle is the curve defined by the parametric equations
 .
.
Why?
Recall that for the acute angle
![]()
which we will call
![]()
in the right triangle below
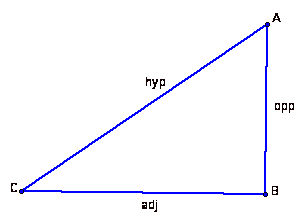
![]()
and
![]() .
.
![]()
In the unit circle which is defined by the equation
![]()
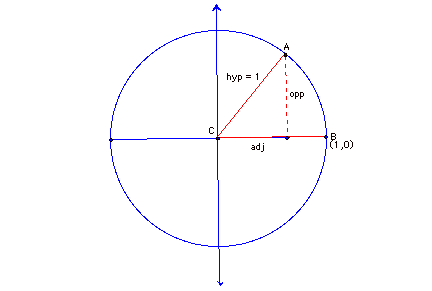
![]()
and
![]() .
.
Recall the graphs of the sine and cosine functions.
![]()
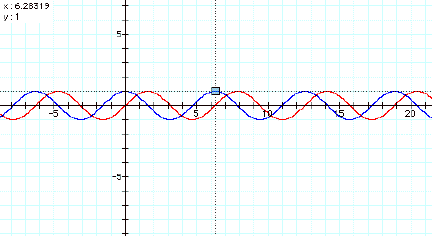
Remember that the graphs are periodic and that they repeat themselves at ≈ every 6.28 units.
. Thus, that is
why
![]()
in the parametric
equations
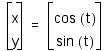 .
.
Notice the following table. Keep in mind that some of the below values are
approximations.
|
t |
x=cos(t) |
y=sin(t) |
|
0 |
1 |
0 |
|
0.52 |
0.87 |
0.5 |
|
0.78 |
0.71 |
0.71 |
|
1.05 |
0.5 |
0.87 |
|
1.57 |
0 |
1 |
|
3.14 |
-1 |
0 |
|
4.71 |
0 |
-1 |
|
6.28 |
1 |
0 |
For each value of t in the table above
![]()
because in the unit circle the cosine and sine are defined as
![]()
and
![]() .
.
Thus, the parametric equations for
![]()
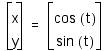
for
![]()
define the unit circle.
![]()