

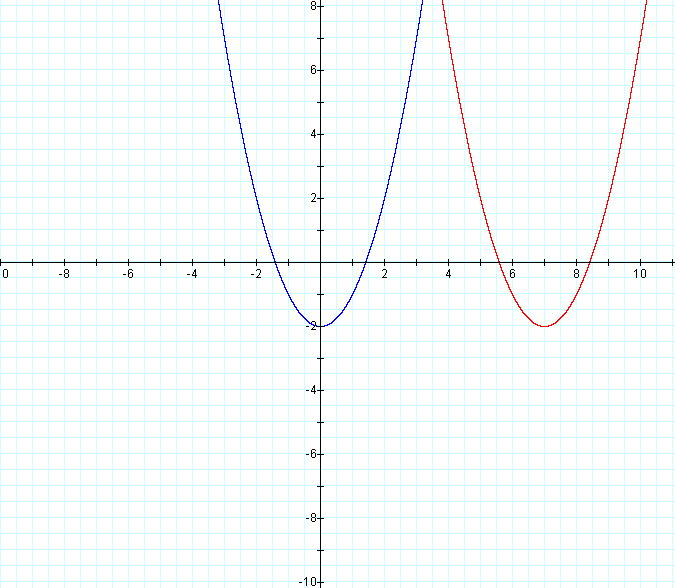
Let's examine equations of the form:

For simplicity's sake when viewing the graphs, we shall restrict d so that
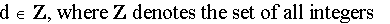
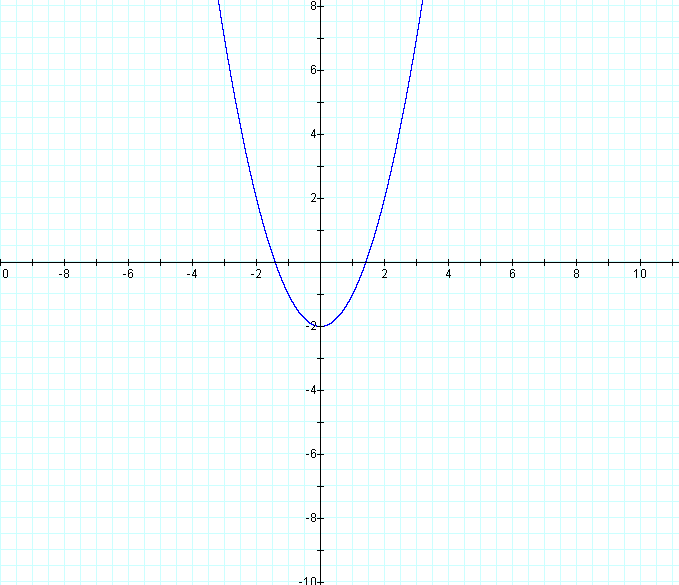
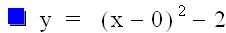
We see that the graph is a parabola. Why is this? If we multiply the right side out, we obtain the equation:
Let's observe some graphs to garner some intuition as to what changing d will do the graph. For a reference, I have included our original graph in each of the following.
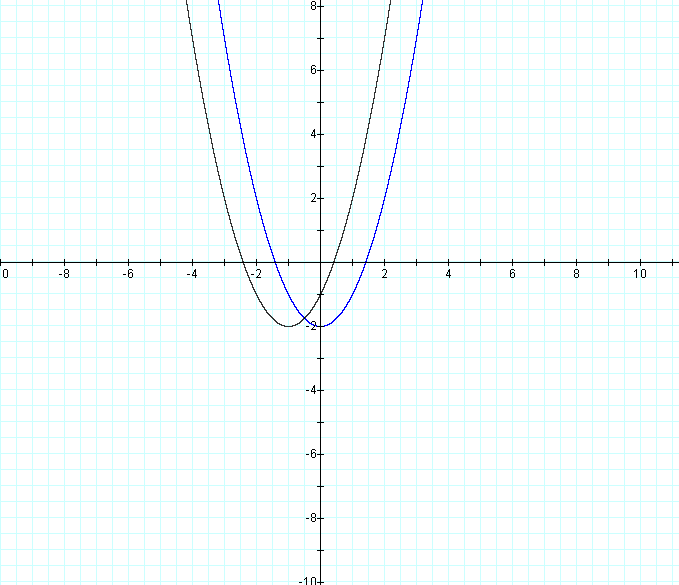
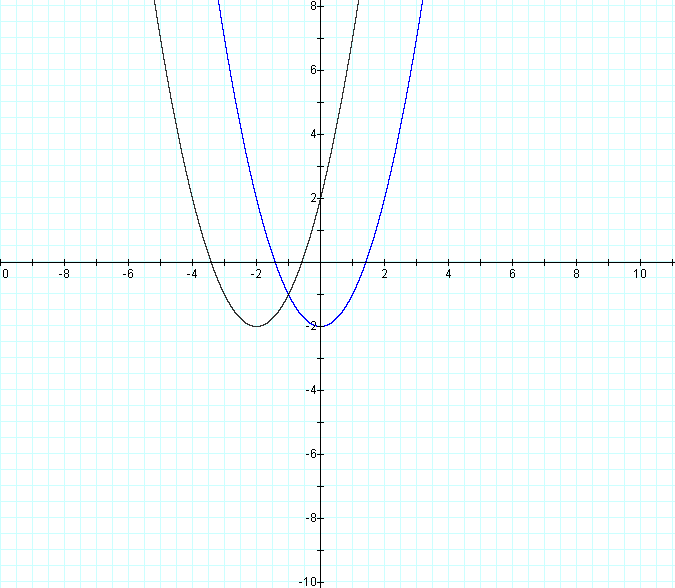
When d = 1, we have
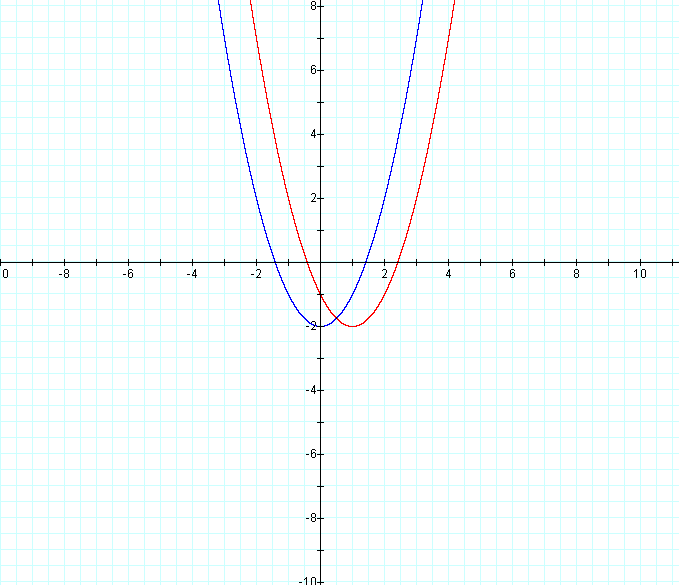
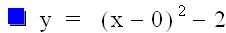
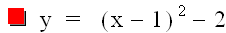
When d = -1, we have
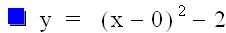
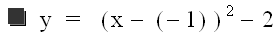
Now let's try, d = 2 ...
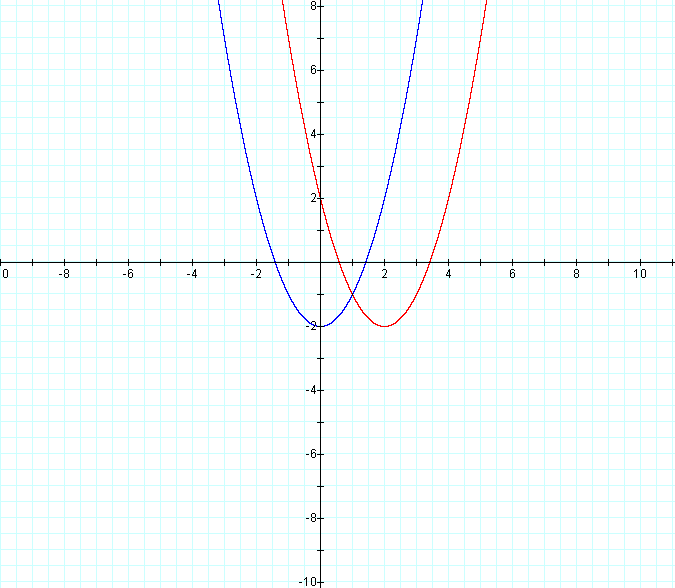
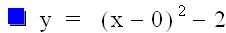
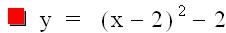
and d = -2
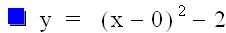
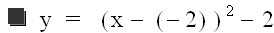
Noticing a pattern? Let's look at two more graphs and then decide...
When d = 3, our graph is
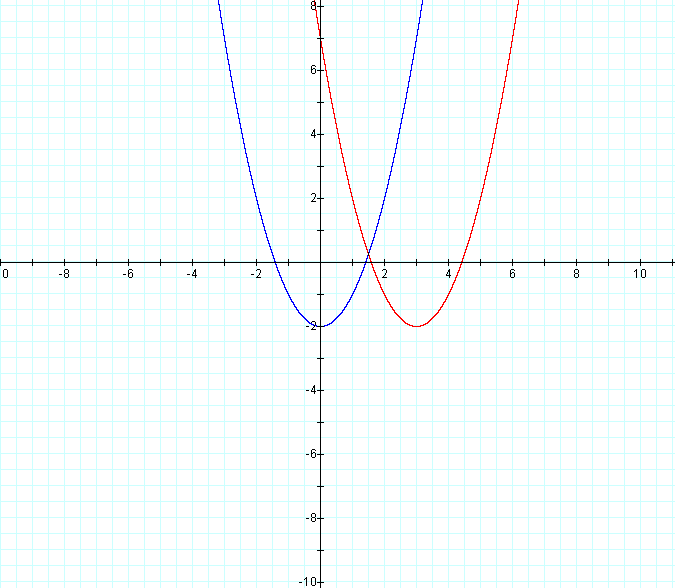
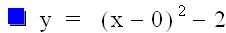
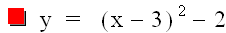
Then for d = -3, our graph becomes
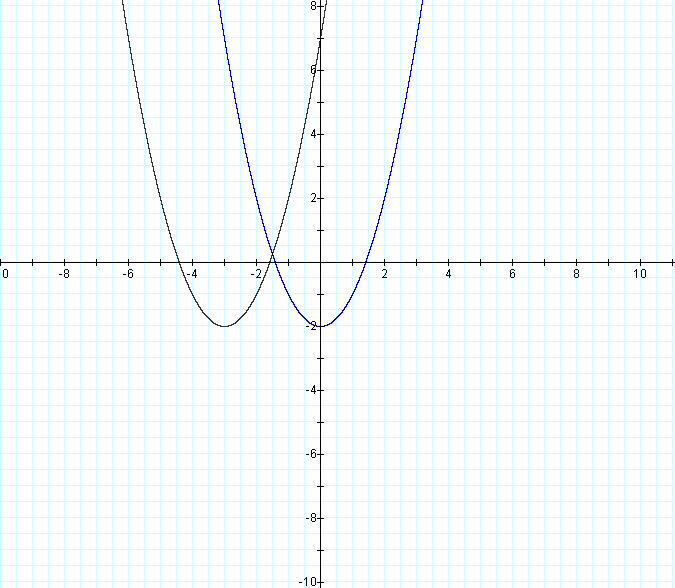
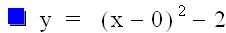
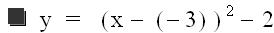
So were you able to decide? Does changing d effect the shape of the graph?
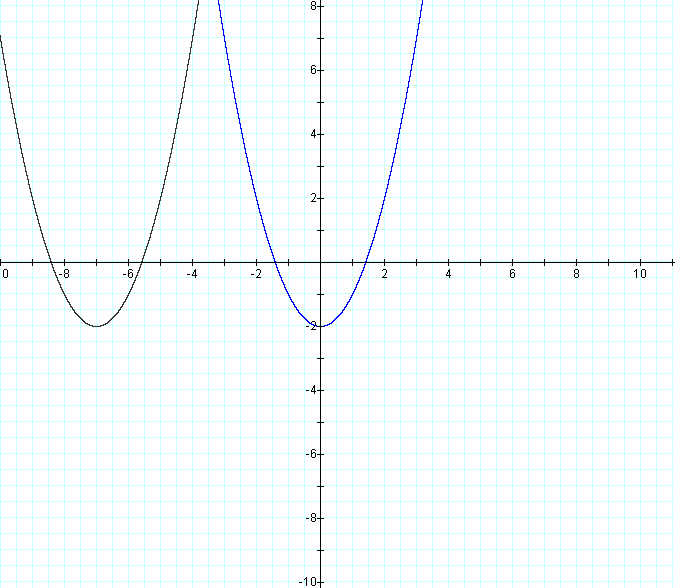
We can see that it does not. The parabola always opens upwards, and it's vertex always
lies on the line y = -2. The only change in the graph is where the vertex is in relation
to x. Notice that the vertex can be found at the coordinates (d, -2) for each graph. So
changing d simply moves the graph right when d is positive, and left when d is negative.
The following graphs further illustrate this relationship.
For d = 7
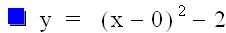
For d = -7
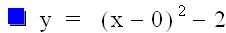
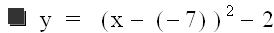
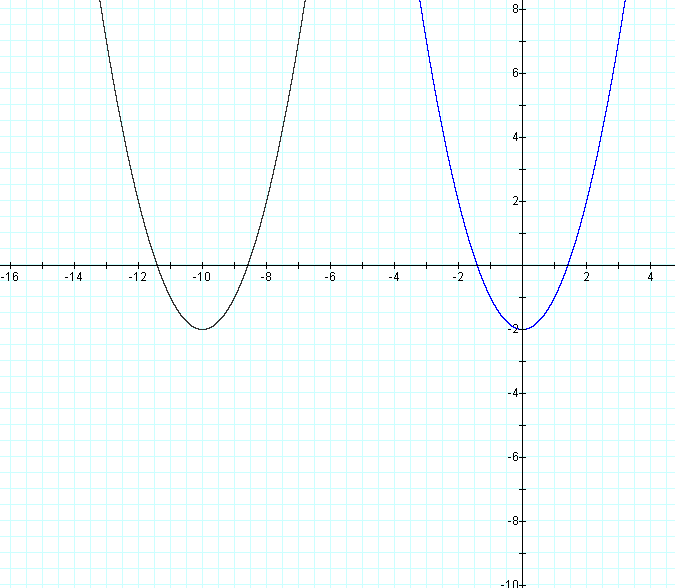
For d = 10
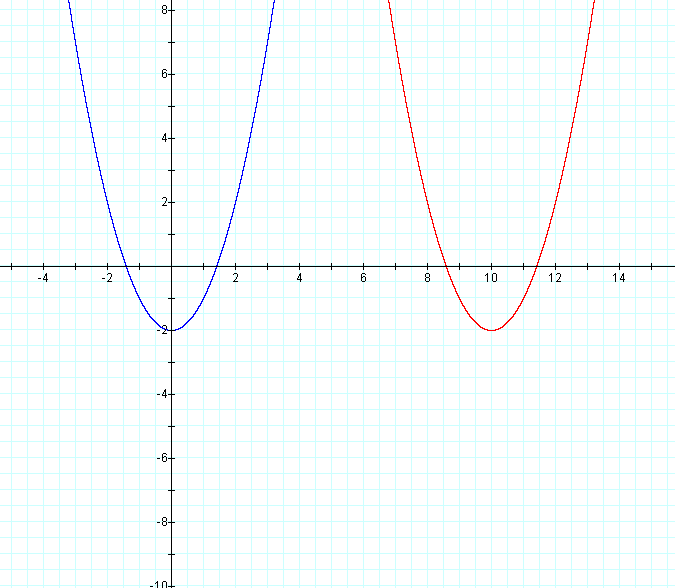
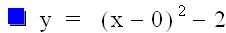
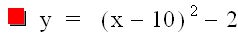
For d = -10
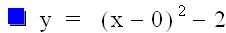
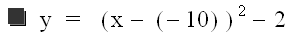
| Return to main page. |