

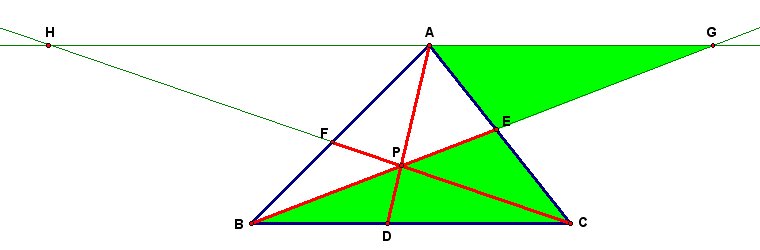
Let's consider any Triangle ABC. We then select any point P in the interior of our Triangle ABC and construct the lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. The following illustration is one such situation.
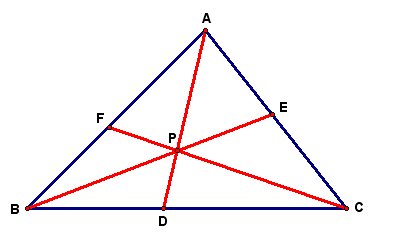
Click here for GSP tool to create a triangle and and these segments when P is inside the trianble. Use this tool to explore different configurations of Triangle ABC. Now explore (AF)(BD)(EC) and (FB)(DC)(EA) for different triangles and various locations of P.
Now we wish to consider the following relationship:
![[(AF)(BD)(CE)]/[(BF)(CD)(AE)]](Image9.jpg)
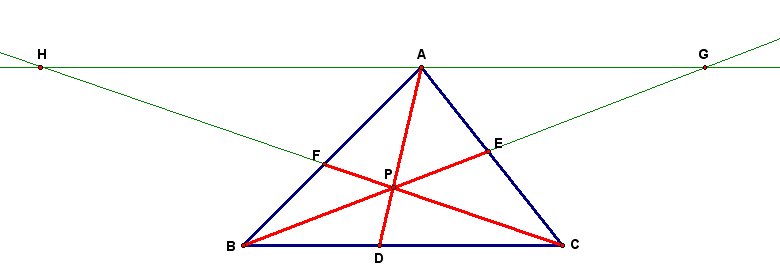
Let us first look at the similar triangles AFH and BFC as shown in the next illustration.
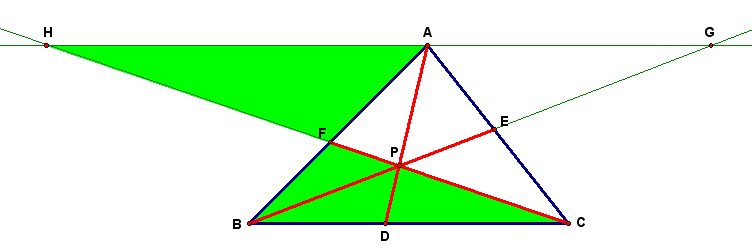
Since corresponding sides of similar triangles are proportional, we obtain the following
relationship:
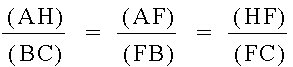
We now obtain this relationship:
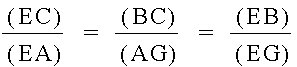
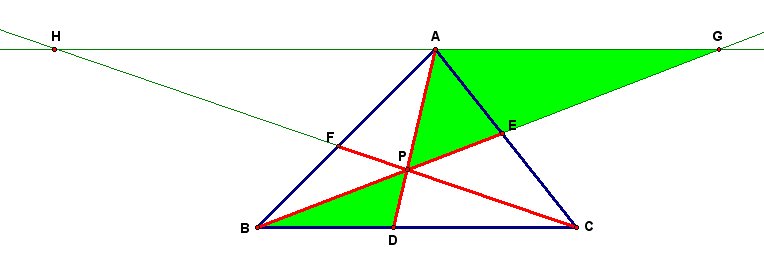
The relationship we find in these similar triangles is:
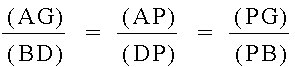
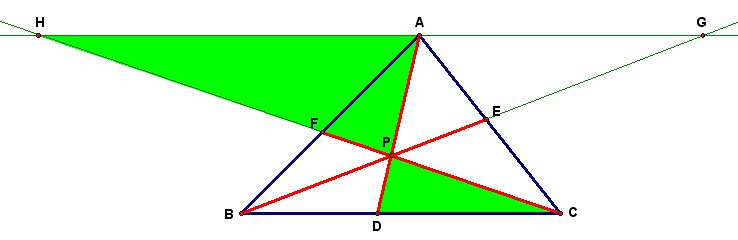
From here we have:
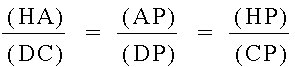
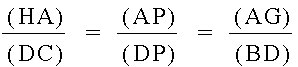
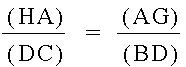
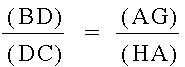
![[(AF)(BD)(CE)]/[(BF)(CD)(AE)] = [(AH)(BC)(AG)]/[(BC)(AG)(HA)]](Image18.jpg)
![[(AF)(BD)(CE)]/[(BF)(CD)(AE)] = 1](Image19.jpg)
We can also extend this to when P is outside of Triangle ABC. The following is one such illustration. Also included is a GSP tool for when point P is outside of the triangle.
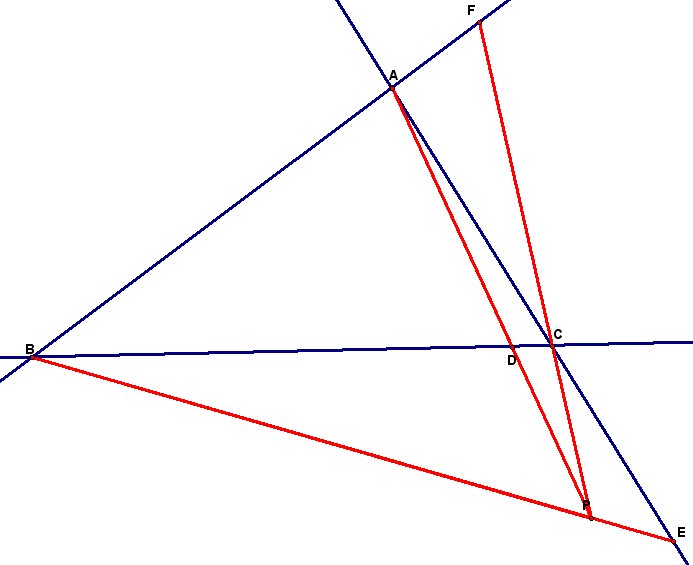
Click here for GSP tool to create a triangle and
and these segments when P is outside the triangle.
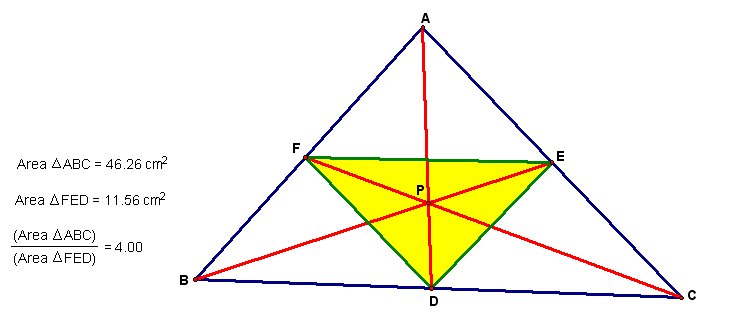
Interestingly, the ratio of the area of Triangle ABC to the area of Triangle DEF is always greater than or equal to 4. Can you come up with the proof on your own? The following illustration shows a configuration where the ratio is equal to 4. Do you recognize the location of point P? Point P is located at the centroid of Triangle ABC. Included below is a GSP file where you can play with the location of point P and see how that affects the ratio of the areas.
Click here for GSP file to explore this relationship..
| Return to main page. |