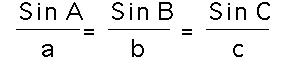The Law of Sines states that

.

We will prove the Law of Sines for the acute triangle case and the obtuse triangle case.

Let's go!

Letbe an acute triangle with . Notice h is the perpendicular from A to the line segment BC. It intersects the segment BC at the point D. Now, two right triangles are formed and they are .

If we want to prove the Law of Sines holds true in this acute case, it is enough to show that.

Remember that the sine of an angle is .

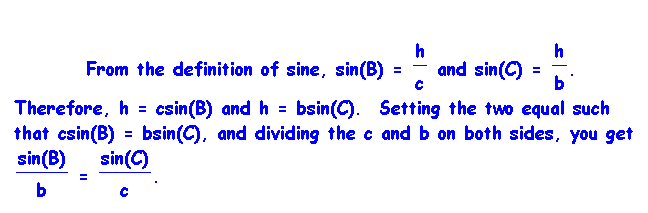
Now we have proved the Law of Sines for the Acute Triangle case!

Let's continue and try to prove the Law of Sines for the Obtuse Triangle case....

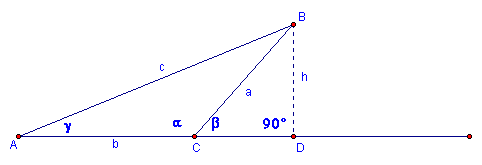
Let be an obtuse triangle with . Notice again that h is the perpendicular from the point B to the line segment AC. H intersects the segment AC at the point D.

Alpha is an obtuse angle and Beta is its supplement. Remember that angles that are supplementary form a line. Therefore, alpha plus Beta form the line with points A,C, and D on it.

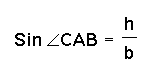and 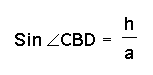so h = bsin and h=asin.

Setting the two h's equal to one another, we get

bsin= asin.

Therefore, 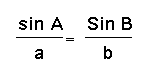and the Law of Sines works for the Obtuse Triangle case as well:)

The Law of Cosines states that

.

We will prove the Law of Cosines for the acute triangle case and the obtuse triangle case.

Let's go!

Remember the cosine of an angle is equal to the .

Segment CD or h is the perpendicular from the point C to the line segment AB. It intersects the line segment AB at the point D.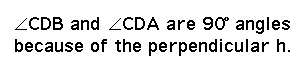

. Therefore, .

Therefore, we have proved the Law of Cosines for the Acute Triangle case.

Using the fact that Triangle ADB and Triangle CDB are both right triangles, we can use the Pythagorean Theorem to get...

Simplifying gives us .

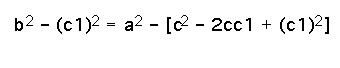
Then finally, . So, we have proved the Law of Cosines for the Obtuse Triangle Case.

RETURN