Final HW (first problem)
Damon Gang
1. Problem set 4, exercise 11:
(a) A line passes through the origin with direction numbers (3,-2), what is its slope?
Since the horizontal change is +3 and the vertical is -2 the slope must be -2/3.
Find the equation of the parallel line through (3,4) (use a vertical translation):
The equation of the original line is (x,y)=(3k,-2k). 3k=3 when k=1 so -2k=-2(1)=-2. To get the y-coordinate of 4 I must add 6 to the -2 so (x,y)=(3k,-2k+6). Thus, the answer here must be (x,y)=(3k,-2k+6).
Do you know what this form of a straight line is called?
We started with the direction numbers (slope) followed by a vertical translation so we must have the equivalent of the slope intercept form of the equation of a line. (x=3k gives k=x/3 so y=-2(x/3)+6 or y=-(2/3)x+6 ie slope intercept form)
More generally use (1,m) and general but fixed point (x1,y1).
Here, (x,y)=(k,mk) so for k=x1 we have y=m(x1) so mk-m(x1)+y1 will work ie. (x,y)=(k,mk-m(x1)+y1) is the desired point form of the line through (x1,y1) parallel to (1,m).
(b) Find the equation of the line that is perpendicular to (1,m) at the origin.
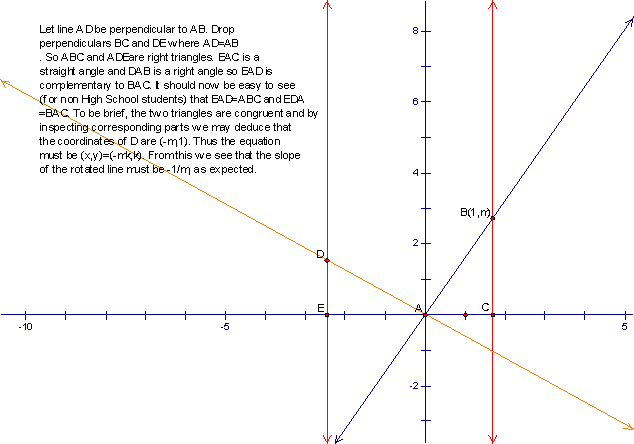
(c) Find the equation of the line perpendicular to m and passing through (-5,-7).
The equation for line m is (x,y)=(k,mk) so by (b) the equation of the perpendicular must be (x,y)=(-mk,k). Now –mk=-5 if k=5/m so k+a=-7 gives 5/m+a=-7 or a=-7-5/m. Thus the equation we are
looking for is (x,y)=(-mk,k-7-5/m).