Review:
1.) We know the interior angles of a triangle add up to _____ degrees.

2.) We also know that the interior angles of a quadrilateral add up to _____degrees.

3.) What about the interior angles of a 2-sided figure? Try to draw this or take a minute and try on geometer's sketchpad.
Let's make a table:
| Number of Sides | Name of Polygon | Sum of Interior Angles |
|
|
Triangle | 180 degrees |
|
|
Quadrilateral | 360 degrees |
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
Can you fill in the rest of the table? For a hint, rewrite the table with 1 more column to find a pattern. The rewritten table is below to help you.
| Number of Sides | Name of Polygon | Sum of interior angles |
|
|
|
|
180 degrees | 1 x 180 |
|
|
|
360 degrees | 2 x 180 |
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
Do you see the pattern now? Here is the finished table with the established generalization:
**The students should see the pattern of numbers from the 1st column to the 4th column.
| Number of Sides | Name of Polygon | Sum of interior angles |
|
|
|
|
180 degrees | 1 x 180 |
|
|
|
360 degrees | 2 x 180 |
|
|
|
540 degrees | 3 x 180 |
|
|
|
720 degrees | 4 x 180 |
|
|
|
900 degrees | 5 x 180 |
|
|
|
1080 degrees | 6 x 180 |
|
|
|
1160 degrees | 7 x 180 |
|
|
|
1440 degrees | 8 x 180 |
|
|
|
1800 degrees | 10 x 180 |
|
|
|
(n - 2)180 |
The first theorem has been established: The sum of the measures of the interior angles of any polygon can be found using the formula:
Where are the exterior angles of a polgon located?
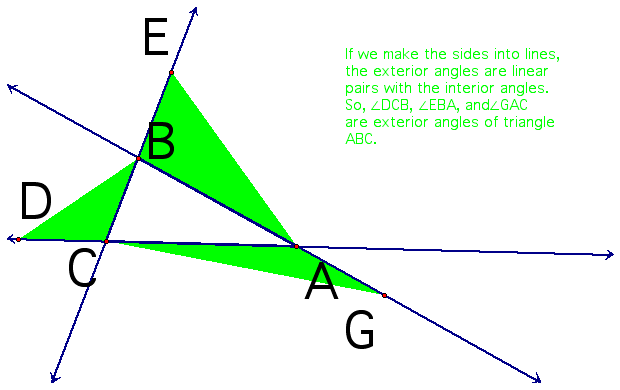
What do you think their sum is?
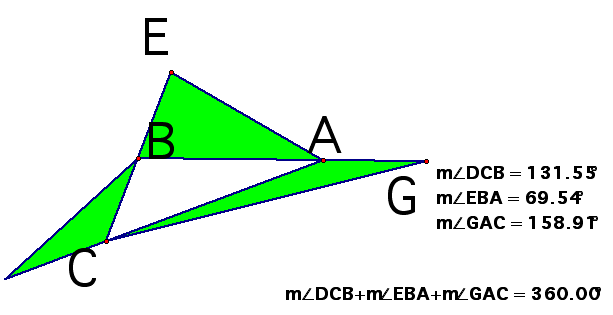
Measuring in geometer's sketchpad, we get that the exterior angles of a triangle add up to 360 degrees.
Assignment #1: Use GSP to find what the exterior angles of other polygons add up to. Use the same table from above and come up with a generalization.
Remember that if a polygon is REGULAR, all sides are congruent and all angles are congruent.
So, could we find the measure of each interior angle of a regular hexagon?
1.) We need to find what the interior angles of a pentagon add up to.
We could look at our chart or quickly calculate (6-2)180 = 720 degrees.
2.) Since each angle is equal, 720 is split into 6 equal parts. So, 720/6 = 120 degrees is the measure of each interior angle.
Let's look at a sketch and measure to make sure!

So, we can see that each individual angle measures 120 degrees and that the sum is 720 degrees.
Assignment #2:
1.) Will all of the angles of every hexagon be 120 degrees?
Draw some pictures and explain your answers.
2.) Make a chart for the measure of each interior angle of all of the polygons that we did above and come up with a generalization.
3.) Do the same type of investigation for the measure of each exterior angle of a regular polygon. Is there a generalization for that?