---

To begin this investigation of parametric curves let us keep in mind that there are limits to the precision of the software used to create the graphs to follow. This mean that the more values of t we use the more precise the graphs will be.

To begin let t range from zero to 2 pi. And look at the graph of

when a = b.

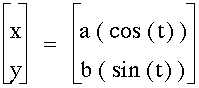
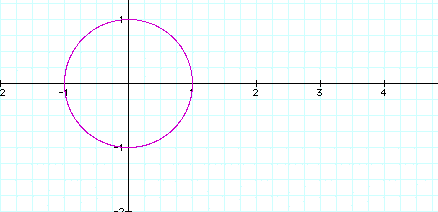
When a = b = n, we get a circle, centered at the origin with radius n.

When a < b                                                 a > b

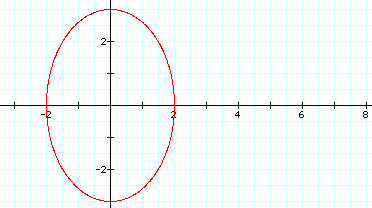
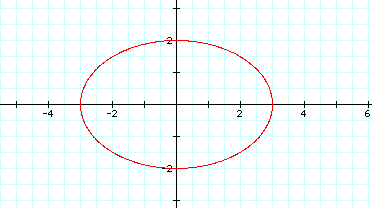
These appear to be ellipses centered at the origin. When a < b the major axis is vertical and when a > b the major axis is horizontal.

What happens if we square the cos and sin?

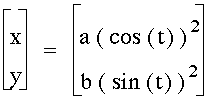if a=b=1

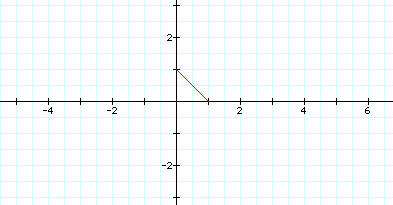
a line segment from ( 0 , 1 ) to ( 1 , 0 ).

If a < b the left and right endpoints of the segment change to ( 0 , b ) and ( a , 0 ) respectively. Similarly if a > b the left and right endpoints of the segement are ( 0 , b ) and ( a , 0 ) respectively.

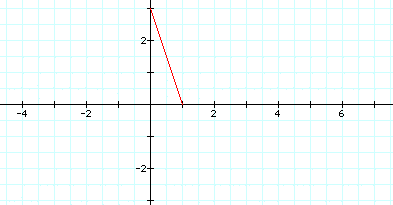
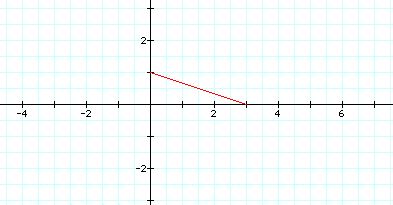
The major change is the change of the slope of the segment. If a < b, the slope increase as the absolute value of the difference of a and b increases and approaches 1 as the difference approaches zero. Likewise, if a > b the slope of the segment decreases as the absolute value of the difference increases, and approaches 1 as the difference approaches zero.

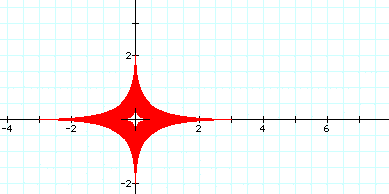
The graph of

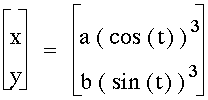is an astroid. If a = b, then the astroid is symmetic about the x and y axis.

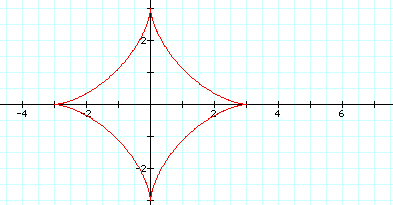
Similar to the ellipses the shape of the astroids are changed as the values of a and b are changed.

For a > b

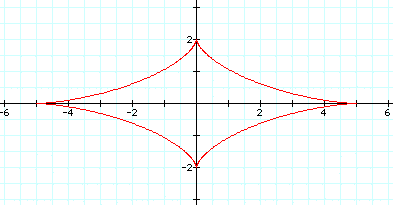the graph is no longer symmetric and there is a horizontal stretch when a > b.

For a < b

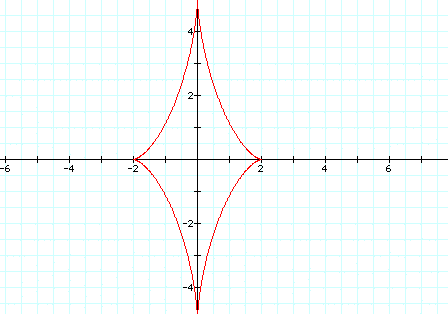the graph is no longer symmetric and there is a vertical stretch when a < b.

The graphs of

is a branch of a hyperbola in the first quadrant. When a = b the graph appears as a smooth curve with left endpoint at (0, b ) and the right endpoint at ( a , 0 ). This is where the precision of the software comes into play. For t between 0 and 2 pi, there is not much to see.

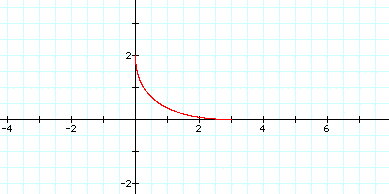However if we increase the range of t an interest graph in seen. Let t range from 0 to 500.

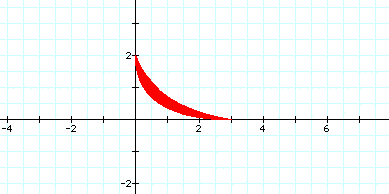
Now let use 5, 6, 7 ,8 as exponents for cos and sin.

For even values of the exponent we get a graph like the one above.

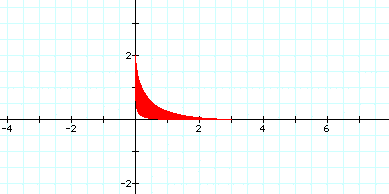
However for odd values of the exponent we get:

The graph fill into the origin if the exponent is odd and greater than 9.