Assignment #4: Centers of a Triangle

By: Keith Schulte

Today's Topic: Centroid and Medians

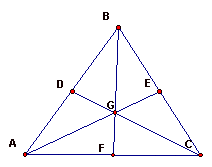
One center of a triangle is the 'Centroid', which is commonly denoted by the letter 'G', because it represents the center of gravity of the triangle. It is created by the intersection of the three medians of a given triangle. By definition: a median of a triangle is a segment from a vertex to the midpoint of the opposite side. In the figure below, we are given triangle ABC. The points (A, B, and C) are the vertices of the triangle. The midpoint of segment AB is point D. The midpoint of segment BC is point E. The midpoint of segment AC is point F. The line drawn from point C to point D is one of the three medians of the triangle. The other two medians of the triangle are the segments AE and BF. The point where the three medians intersect is the CENTROID, point G. If the triangle was cut-out on a piece of cardboard, like the figure below, we should be able to balance the triangle, by placing our finger underneath point G.

What other relationships can we determine with regard to the Centroid and medians? If we create segments connecting the midpoints of triangle ABC above, we would create a new triangle inside of the original triangle with vertices at points D, E and F, see below

The new triangle, in red above, is called the MEDIAL Triangle. We found above that point G is the center of triangle ABC. By identifying the midpoints of each side of the triangle and then creating a segment from a vertex to the midpoint on the opposite side of the triangle. Is the relationship of G to the new triangle the same as it was to the original triangle? That is, is G the center of gravity of the Medial Triangle and the original triangle? Let's identify the midpoints of the Medial Triangle and create segments between the vertices and the midpoints and see if the intersection is the point G!

We see that point G is the center of the medial triangle! If we made a medial triangle inside of this medial triangle, would point G be its center also?

By creating the new triangle with segments connecting the midpoints of the previous triangle, then finding the midpoints of the new triangle and connecting the new midpoints to the vertices of the new triangle, we find that point G is the center of the new triangle as well. If we continued to make smaller and smaller medial triangles, we would always find G to be the center of those triangles as well.