
Constructing a Parabola
By
Audrey V. Simmons
Parabolas are usually graphed by using the quadratic equation given for the particular situation. We know that if the equation is written in vertex form
y = a(x-h)2 + k that the vertex is (h,k). Values of a and k tell us other information about the shape of the graph. We can plot additional values and draw the graph.
Sometimes the
quadratic equation is written in standard form y= ax2 + bx + c . In this case, we know that the value for h (x value in the vertex) is equal to ![]() . We can use h
to find the value of k (our y coordinate). By substituting other values for x and
y we can draw the graph.
. We can use h
to find the value of k (our y coordinate). By substituting other values for x and
y we can draw the graph.
This time we would like to construct a parabola. By definition, a parabola is a set of points (locus) equidistant from a line and a fixed point. The line is called the directrix. The fixed point is called the focus. We will pick our focus so that it is not on the directrix.
Step 1
Draw a line. Pick an arbitrary point F that is not on the line.
Step 2
Pick another arbitrary point called P in this illustration. This time the point should be on the directrix. Draw a perpendicular line from point P. We will be using this line to find a point that is equidistant from both the directrix and the focus.

Step 3
Draw a segment connecting our focus (F) with the arbitrary point (P) on the directrix. Find the midpoint of this segment and draw a perpendicular line through that point. Remember all points on this line will be equidistant from both the focus and point P.
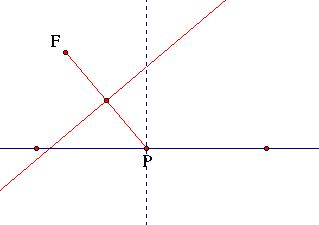
Step 4
Since all points on the perpendicular bisector are the same distance from F and P we can draw an isosceles triangle with points F, P, X. The point where the perpendicular bisector and the perpendicular to the directrix intersect is a point on the parabola.
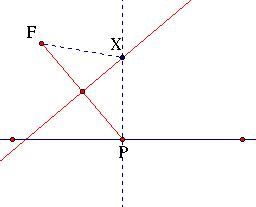
Step 5
To see the parabola or locus of points equidistant form both the directrix and the focus click HERE.
Step 6
To see a trace of the tangent line constructed at the constructed point click HERE.
Step 7
Click HERE to see the locus command.