Investigating Second Order Polynomials
By: Stephen Bismarck
Produce several ( 5 to 10) graphs of
y = (x-d)2 - 2
on the same axes using different
values for d. Does varying d change the shape of the graph? the
position?
The first thing I did for this problem was pick some values for d.
I picked d = -10,-3,0,2,3,10
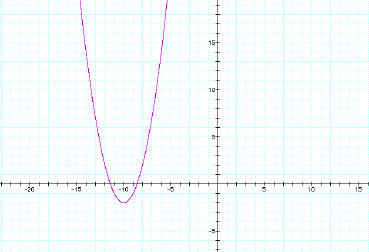
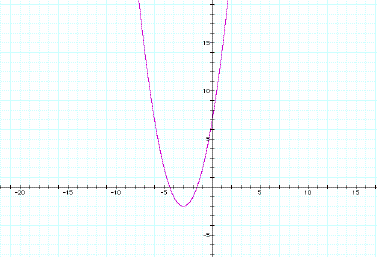
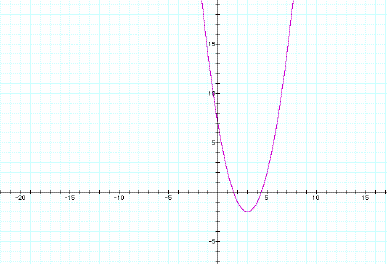
y = (x +10)2
– 2 y
= (x + 3)2 – 2
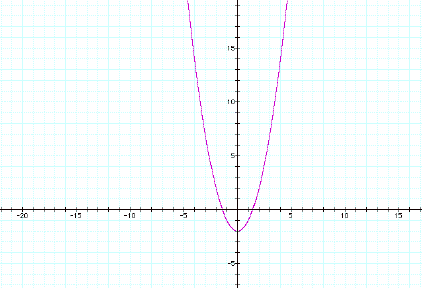
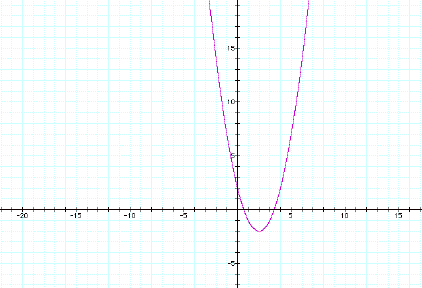
y = x2 – 2 y
= (x – 2)2 – 2
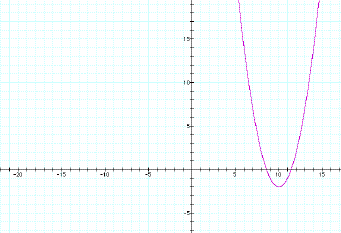
y = (x – 3)2
– 2 y
= (x + 10)2 - 2
As you can see from these
graphs, the parabola does not change shape (it does not get larger or smaller)
the only thing that happens is that it changes positions. The next graph shows this fact much
better.
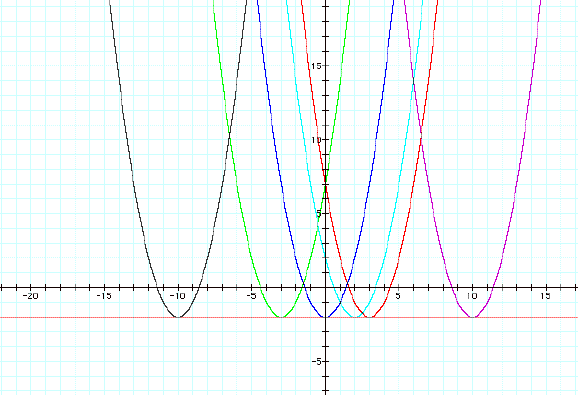
I have also
included the line y = -2 to illustrate the parabolas movement. Each of
the vertices land on the line y = -2, so that means the y coordinate will
always be –2. This is easy to show by calculus or the form that the
equation is in. Let me start with the harder of the two calculus.
To find the
extrema of any second-degree equation you need to take the derivative.
___________________________________
Calculus
Version
y = (x – d)2 – 2
y’ = 2(x
– d) = 2x – 2d
2x – 2d = 0
x = d
Plug back into
original to find y value for exterma
y = (d – d)2 – 2
y = -2
So the vertex of
the parabola is always going to be of the form (d, -2)
Easy Way
If you look at
the equation it is in the form y = (x – h)2 + k,
where (h, k) is the vertex of the parabola.
Since we have y =
(x – d)2 – 2, the vertex must be (d, -2).
