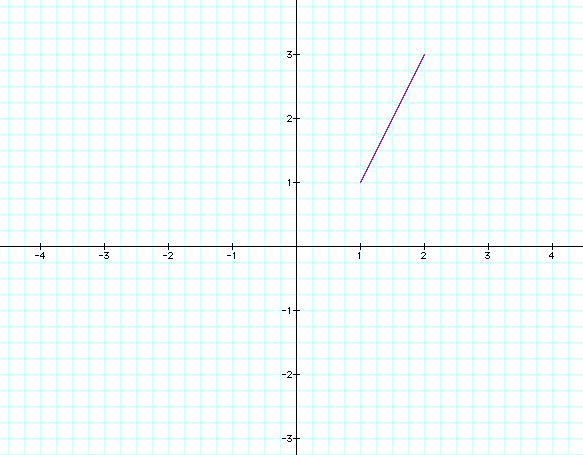
Graph x=t+1, y=2t-1 for some appropriate range for t.
Interpret. Is there anything to vary to help
understand the graph?
The graph of x=t+1, y=2t-1 is shown below with the range [0,1] for t.

Notice that the equations appear to make a line segment. Let's try a different range such as [-1,1] to see if anything changes?
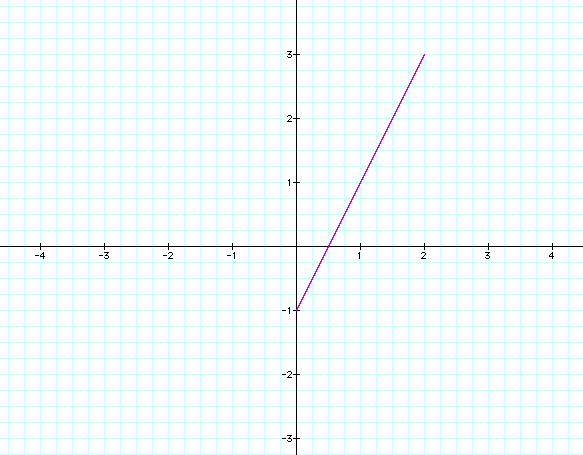
Now we have some negative values, but it is still only a line segment. What happens if we increase the range to [-10,10]?
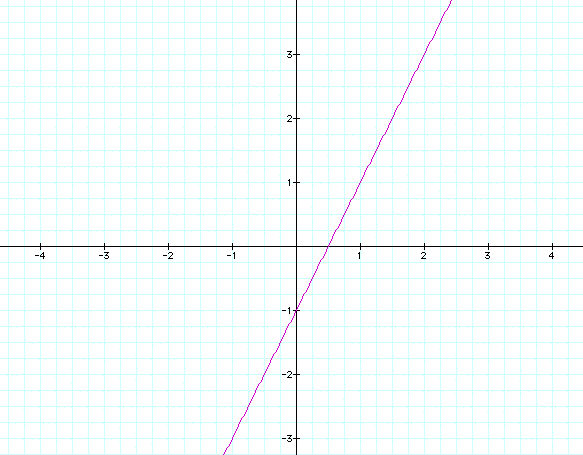
It now appears that we have a line. But after zooming out you will see that we still have a line segment which is shown below.
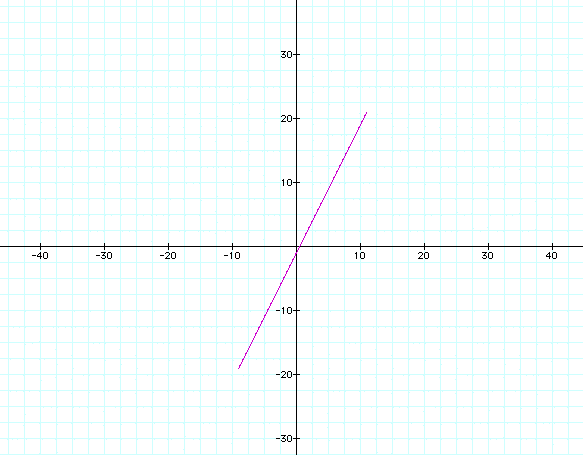
Will we always get a segment? Let's now try a large range of t such as 1000.
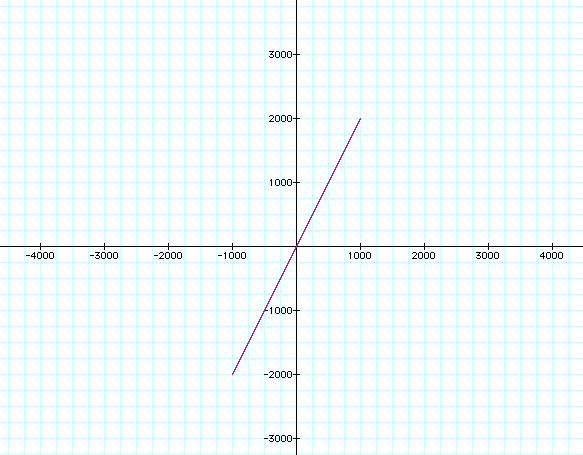
Again, we get a segment. So the question is how to get a line. We can try setting the two equations x and y equal to each other and solving for t. After doing this, we get:
Now we can graph y=2x+3
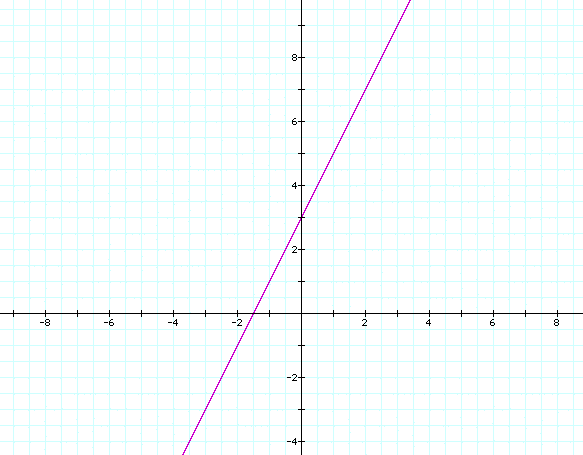
We finally get a LINE!! So now we come to the
conclusion that parametric equations are only pieces of a function.