Explorations of Pedal Triangles

By Lauren Lee

What is a pedal triangle? Let triangle ABC be any triangle. If P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC is the pedal triangle for the point P.

Let’s look at a construction:

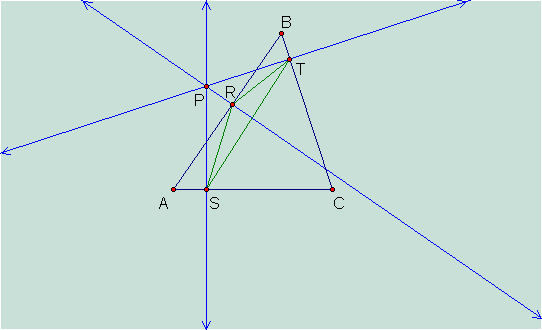
I have labeled the points of intersection R,S, T. So triangle RST is the pedal triangle for the pedal point P

_____________________________________________________________

What if P is the orthocenter of triangle ABC?

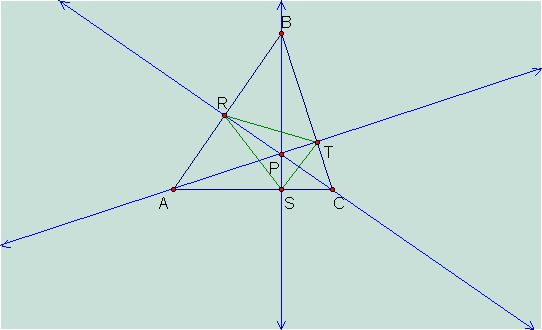
We notice that P lies on the angle bisectors of the pedal triangle RST

_____________________________________________________________

What if the orthocenter is outside of triangle ABC?

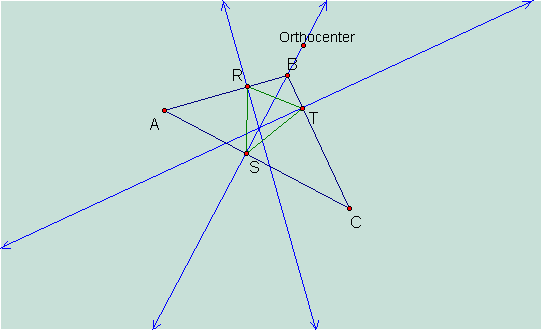
The pedal triangle RST still lies inside triangle ABC

_____________________________________________________________

What if P is on the side of triangle ABC?

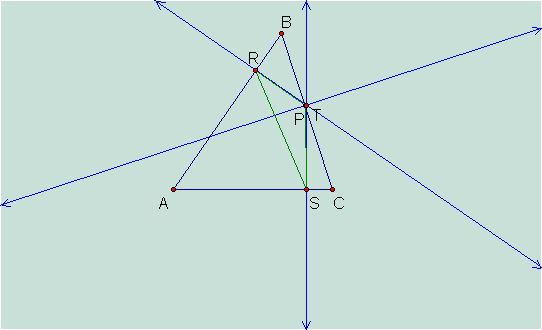
We can see that P becomes one of the vertices, in this case T, of the pedal triangle RST

_____________________________________________________________

What happens if P is one of the vertices of the triangle ABC?

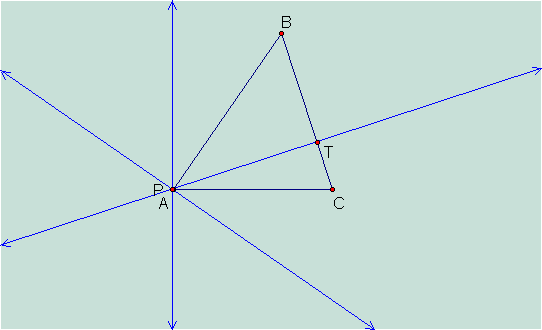
We will notice that the pedal triangle RST collapses. We are left with one of the perpendiculars of pedal point P.

Let’s do one final investigation. What if P was the incenter of triangle ABC?

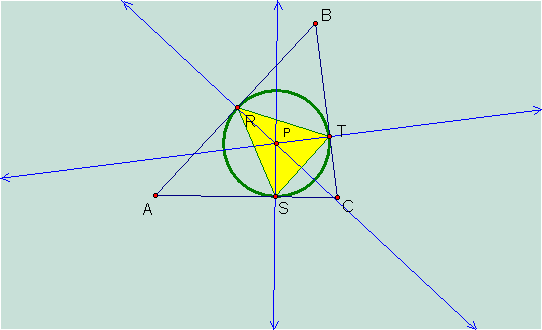
We notice that P is the circumcenter for the pedal triangle RST

Return