EMAT6680 Assignment 12

Spreadsheet Problem

By Kevin Perry

Solving Problems Using Spreadsheets

In this discussion we will investigate the use of the spreadsheet program in solving mathematical problems.

The Spreadsheet

The spreadsheet is a computational tool that started about the same time as computers. Accountants everywhere were used to organizing long columns of numbers to tabulate income and liabilities. The developers of the spreadsheet were determined to help perform those calculations, and in the mean time created a useful tool for all mathematics.

The spreadsheet is organized into rows and columns of cells. In each cell, you can place a fixed number, a piece of text, or most importantly, a formula based on other cells. Therefore, you can create rows upon rows of calculations based on a few simple entries.

Spreadsheet programs now offer graphing functions also. So we can then create graphs based off of the numbers that were created by the formulas.

A Simple Example

A simple way to use the spreadsheet is to compute and graph a function of the form y = f(x). The method is to simply create a column of x values, and put the function in the next column. Let’s take a simple formula like

We first need to create the column of x values. For our purposes, we will use the integer x values from -5 to 5. If we put them into a spreadsheet as a column of numbers, it looks like

x	y=f(x)
-5
-4
-3
-2
-1
0
1
2
3
4
5

We then enter the formula for the y values in the next column under y = f(x). We can enter it once, and then copy it down to fill the column. When we do that, we get

x	y=f(x)
-5	0
-4	-4
-3	-6
-2	-6
-1	-4
0	0
1	6
2	14
3	24
4	36
5	50

We now have the values of f(x) for the x that we entered into the column. We can then graph the points in a scatter plot with line segments connecting the points and we get

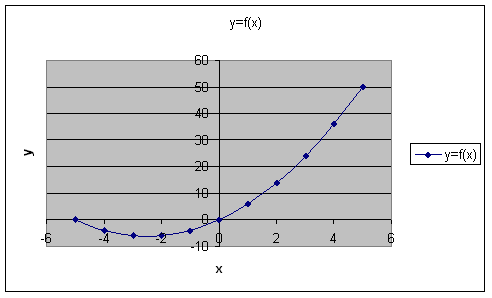
We can see from the graph that we have started to trace out a parabola, and we can see from the data points in the table that the two zeros of f(x) are at -5 and 0.

A Spreadsheet Problem

A good problem to use the spreadsheet for is the following:

What is the largest volume of a lidless box that can be created using a 5” x 8” piece of cardboard if the box is created by cutting a square out of each corner of the cardboard?

The picture of the piece of cardboard with the squares marked for cutting would look like

If you would like to experiment with what the cardboard would look like by cutting larger or smaller squares, click this GSP file.

So how are we going to use the spread sheet to help us solve this problem? Simple, we are going to let it calculate the volumes for lots of different box sizes, and then we can pick the largest value, and hopefully see some sort of pattern.

First, we need to determine the formula the spreadsheet will calculate. The only real variable we have in this problem is the size of the square in each corner. If we call the side of the square x, then the rest of the variables can be determined.

If we fold up the box as follows from the drawing, we see that the width of the box is 5”- x – x, because two squares are cut from the width of the cardboard. The length of the box will be 8”- x – x for the same reason. The height of the box is simply the length of the side of the square and therefore is x. So the formula for the volume of the box given the length of the side of the square is

We could multiply out this formula and try to find a maximum point and all sorts of other complicated things, or we can use the spreadsheet.

To start the spreadsheet, we need to determine what values of x we want to use. From the drawing, it is obvious that the length of the side of the square can be anywhere between 0 and half of the width of the cardboard. Therefore, x is between 0 and 2.5. For our purposes, we will take values of x that are separated by 0.1. The x column of the spread sheet therefore looks like

x	Volume
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2
2.1
2.2
2.3
2.4
2.5

Now, if we add in the formula for the volume, and copy it all the way down, we get

x	Volume
0	0
0.1	3.744
0.2	6.992
0.3	9.768
0.4	12.096
0.5	14
0.6	15.504
0.7	16.632
0.8	17.408
0.9	17.856
1	18
1.1	17.864
1.2	17.472
1.3	16.848
1.4	16.016
1.5	15
1.6	13.824
1.7	12.512
1.8	11.088
1.9	9.576
2	8
2.1	6.384
2.2	4.752
2.3	3.128
2.4	1.536
2.5	0

From our data, we see that if the length of the side of the square is 1”, then we get a box with volume 18 cubic inches. That is the largest value that we calculated, but how can we be sure that the volume can be larger with some x that we didn’t calculate. First, we can use the program to graph all these points, so that we can see if there is a pattern. The graph looks like

From the graph, the volume definitely has a maximum somewhere around x = 1, but we should make sure that it is exactly 1 by changing the resolution of our table.

So this time, we use x going from 0.9 to 1.1 with a resolution of 0.01”. The resulting table looks like

x	Volume
0.9	17.856
0.91	17.88368
0.92	17.90835
0.93	17.93003
0.94	17.94874
0.95	17.9645
0.96	17.97734
0.97	17.98729
0.98	17.99437
0.99	17.9986
1	18
1.01	17.9986
1.02	17.99443
1.03	17.98751
1.04	17.97786
1.05	17.9655
1.06	17.95046
1.07	17.93277
1.08	17.91245
1.09	17.88952
1.1	17.864

And from this table we see that 18 cubic inches is indeed a very good answer for the question.

Conclusions and Extensions

The spreadsheet is a very powerful tool for computing large amounts of calculations quickly and easily. There are a variety of problems that can be solved using a spreadsheet and a little extra knowledge of mathematics.

Return to my homepage.