

There are three graphs here. The two straight lines are g(x) = ax+(1-b) and f(x) = -ax + b. The third graph, h(x) = g(x).f(x)
Notice that g(x) and f(x) represent different straight lines. Thus, for different values of a and b, we get different straight lines which intersect each other and, more interestingly, are tangential to the curve represented by h(x) = g(x).f(x)
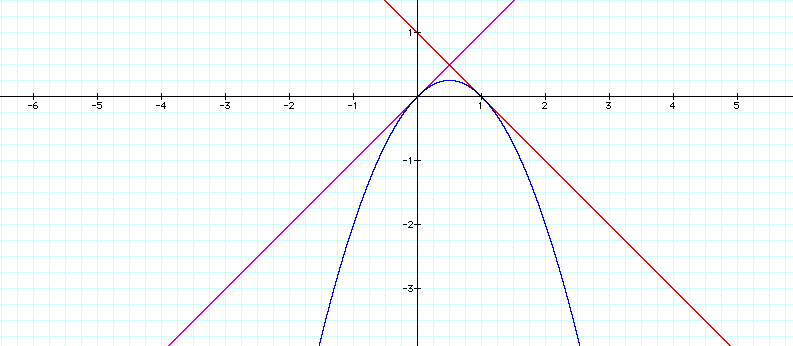
But how did we arrive at these two functions g(x) and f(x) ? Well, we first set out to find two functions g(x) and f(x) such that inersect each other and their product, g(x).f(x) would be tangential to both g(x) and f(x) at exactly one point.
Suppose, we started off with two functions, y = ax+b and y = cx + d
When would they inersect each other? Obviously when the slope of one line is different from that of the other. This tells us that if the two functions were to be of the form, y = ax+b and y = cx+d, it would ensure that they intersect one another so long as a is not equal to c. In the special case when a = -1/c, the lines would be perpendicular to one another.
We now come to the part that necessitates that their product, h(x) be tangential to both of them at one point.
h(x) is given by (ax+b)(cx+d).
We also know that at the point of tangency, the slope of the straight lines will be equal to the first derivative of h(x)
h'(x) = 2acx+ad + bc
From the first straight line, f(x), its a, must be equal to 2acx1 + ad + bc
From the second straight line, g(x), its slope, c must be equal to 2acx2 + ad + bc
We can also take one case when a = -c. In this case, we arrive at b = 1-d
The two functions f(x) and g(x) would then be : f(x) = ax + 1-b and g(x) = -ax + b.
h(x) would then be (ax+1-b)(-ax+b) and would be tangential to f(x) and g(x).