Consider the equation
, where a = 1 and c = 1.
Now graph this relation
in the xb plane. So, 
. We have the following
graph.
If we take any particular value of b, say b = 4, and overlay this equation on the graph we add a line parallel to the x-axis. If it intersects the curve in the xb plane the intersection points correspond to the roots of the original equation for that value of b. We have the following graph.
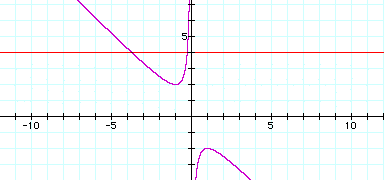
For each value of b we select, we get a horizontal line. It is clear on a single graph that we get two negative real roots of the original equation when b > 2, one negative real root when b = 2, no real roots for -2 < b < 2, One positive real root when b = -2, and two positive real roots when b < -2.
Consider the case when
a=1 and c = - 1. So, 
.
Now graph this relation
in the xb plane. Now 
. We have the following
graph.
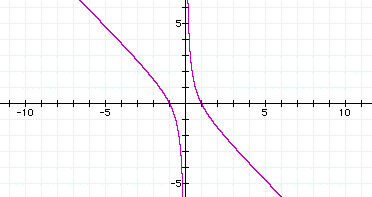
If we take any particular value of b, say b = 4, and overlay this equation on the graph we again add a line parallel to the x-axis. We have the following graph.
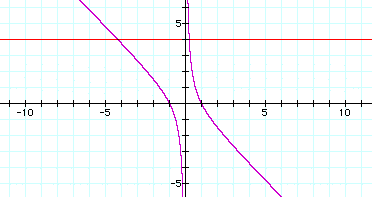
For each value of b we select, we get a horizontal line. It is clear on a single graph that we get one negative real root and one positive real root for all values of b.
Now let's consider other values of c and generalize. Click play below to see an animation for values of c. The blue graph is for c = 1, the purple graph is for c = - 1 and the red is for varying values of c.
From this animation we can conclude that different c-values have a different number of solutions for b.
If c < 0, there will always be one positive real root and one negative real root for b.
If c = 0, there will be exactly one real root for b.
If c > 0, there are some vales of b with two real roots and some values of b with no real roots.
Let's look at this closer. Considering the discriminant of the quadratic formula when a = 1 and c > 0, we have
. When the discriminant is negative is when there is no real solution, so when
there is no real solution for the values of b such that
. We can conclude for the original equation when...
: two negative real roots;
: one negative real root;
: one positive real root;
: two positive real roots.