Exploring the Circumcenter

Assignment 4:
#3. The circumcenter (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. Note: C may be outside of the triangle.
Construct the circumcenter C and explore its location for various shapes of triangles. It is the center of the circumcircle (the circumscribed circle) of the triangle.
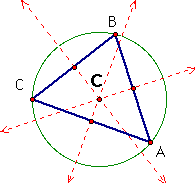
i. My first example is an equilateral triangle, a special case of an acute triangle. The perpendicular bisectors for each side intersect with the opposite vertex. The circumcenter, C, lies on the inside of the triangle. I have also constructed the circumcircle of the triangle.

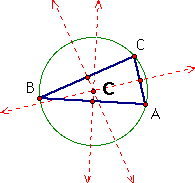
ii. Now I have an obtuse triangle. The circumcenter, C, is outside of the triangle since the perpendicular bisectors intersect outside of the triangle. I have also constructed the circumcircle of the triangle.

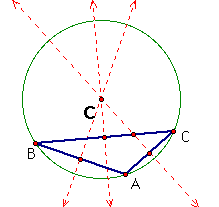

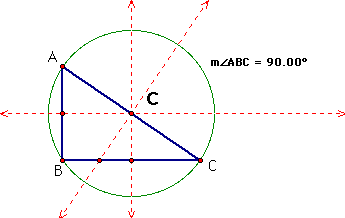
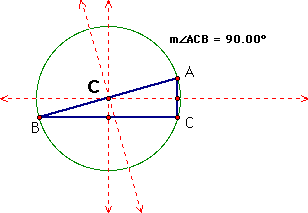
iii. Here is a right triangle. The circumcenter, C, intersects the midpoint of the hypotenuse. In this case the hypotenuse of the triangle is a diameter of the circumcircle.