Department of Mathematics Education

EMAT 6690, J. Wilson

The Pipeline Problem

By Matt Tumlin

To find the Rectangular Cost function, first I had to find the cost of installation per foot on each type of terrain, the normal and wetland. It is given that the pipe itself is two inch coated pipe and costs $1.50 per foot. The instillation cost is $1.20 per foot, thus the total cost on normal terrain is $1.50 + $1.20 per foot, which is $2.70 per foot. It is also given that in a 10 hour day the Track Hoe can dig 300 feet of trench in the wetland. This is the 30 feet per hour. It is also given that the Track Hoe costs $60.00 per hour. Divide $60.00 per hour by the 30 feet per hour and you get $2.00 per foot. Add all the costs together, $2.00 + $1.50 + $1.20 and the result is $4.70 per foot in the wetland. Thus the total cost of installation is equal to 2.7 times the distance on normal terrain plus 4.7 times the total distance in the wetland.

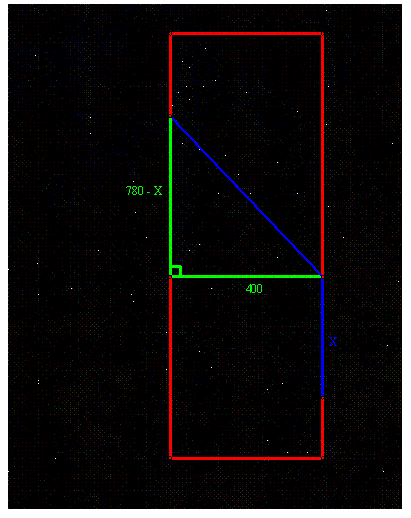
In this equation, x is the distance on normal terrain, while y is the distance in the wetland. Now, I need y in terms of x. The total width of the wetland is 400 feet, while the distance from A to the point perpendicularly from B is 780 feet. By forming a right triangle with the hypotenuse as the distance across the wetland, we can find this distance by the Pythagorean Theorem.

Thus, this distance is equal to

I now have all the elements for the equation. The routes that this equation covers are any routes that come south from A, north from B, or both, and crosses the wetland at any angle.

One question you might ask is, are there any restrictions on x?

Return to Matt’s Pipeline Problem