Department of Mathematics Education

EMAT 6690, J. Wilson

The Pipeline Problem

By Matt Tumlin

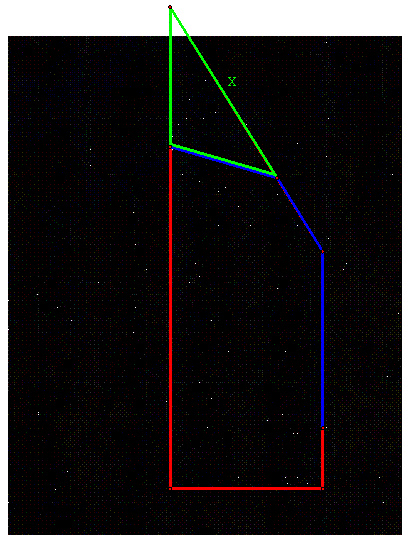
To find the Trapezoid Cost function, I will use the total cost of installation is equal to 2.7 times the distance on normal terrain plus 4.7 times the total distance in the wetland, which I derived earlier.

I now have to find the distance inside the wetland that the pipeline travels. This is done by the Law of Cosine on the triangle created by the pipeline and the trapezoid.

The distance of the pipeline equals:

given by the Law of Cosine. We now have to find the distance traveled on normal terrain. On the angled portion of the trapezoid, the distance is simply:

because x is the other portion of that line and the distance from point B to the northern most point on the eastern side is always 350 feet. We now have the elements to make the cost function. As stated earlier, the cost per foot in the wetland is 4.7 and the cost per foot on normal terrain is 2.7. Thus we multiply the corresponding prices with the lengths and we get the equation.

Return to Matt’s Pipeline Problem