Assignment 1

By: J. Matt Tumlin, Cara Haskins, & Robin Kirkham

Examine graphs of y = a sin(bx + c) for different values of a, b, and c.

Our first step will be to look at the basic sine graph

when a=1, b=1 and c=0.

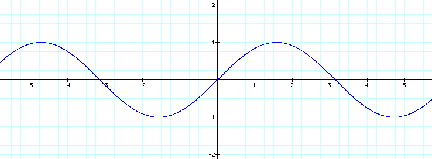
Notice that the Domain is the set of real numbers, and the Range is [-1,1]. The graph of the sine function continues indefinitely.

The amplitude is the distance from the axis to the highest or lowest point, or it is half the distance from the highest to the lowest point. Let us use during this example the variable “a” in demonstrating the amplitude which is currently a = 1.

The period is the time it takes for the graph to make one complete cycle or in other words, the amount of time it takes for the graph to begin repeating. Let use the variable “b” in conjunction with adjusting the period. In this case the period is 2p.

In our example, the sine wave phase is controlled by the variable “c”. Which in this first case, c = 0.

Continue to use the basic sine graph as our frame of reference. Let us examine what happens to the graph under the following guidelines.

Step 1: a sin (bx +c)

Let b=1,c=0, and vary the values of a. Our new equation becomes

y=a sin(x).

Let us use Graphing Calculator 3.2 to examine the effects of using different values for a , remembering to use positive and negative values.

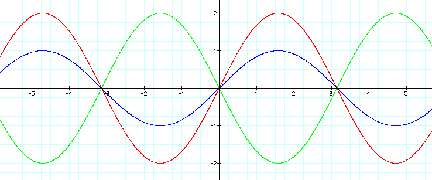
The blue graph is y=sin x. This basic sine graph will always be in blue in future examples for comparison purposes.

Notice when the value for “a” is positive, the amplitude increases by a factor of the absolute value of "a", and the graph emulates the y = sin x graph as demonstrated above. This is known as a vertical stretch. Similarly, when the variable "a" is negative, the amplitude is still increased by the absolute value of “a”. However, the negative value of "a" causes the graph to be reflected across the x-axis.

Step 2: Now we are examining the effects of variable “b”. Let a=1, and c=0 and change the values for b. Our new equation is now:

y = sin (bx).

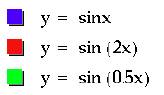
Notice that the amplitude of the graphs does not change even though the value for b was varied. When “b” > 1, the period of the graph is changed to 2p/b, resulting in a horizontal shrinking of the graph. When 0 < “b” < 1, then the period is still changed to 2p/b, however the graph is now stretched.

This leaves the question what happens when negative values are substituted for variable “b”?

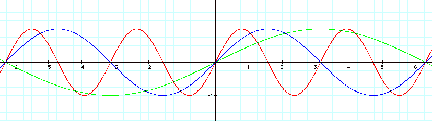
By substituting negative values for “b”, notice there is a reflection across the x-axis for our two graphs as well as a horizontal change of the basic sine graph.

Step 3: Let us start again with our original equation y= asin(bx+c). Let a=1, b=1, and vary c, resulting in:

y = sin(x+c)

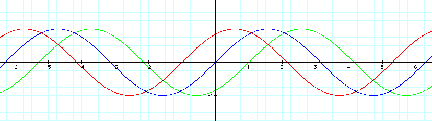
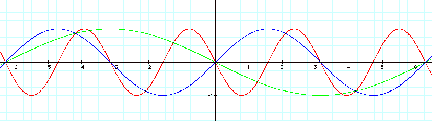
The value of variable “c” moves the sine graph to the right or the left. When “c” > 0, the graph moves to the left. When “c” < 0, the graph moves to the right.

This horizontal movement is called the phase shift. The phase shift appears to be equal to the value of “-c”.

To be sure, let us check what happens to a change of variable “b” and “c” simultaneously.

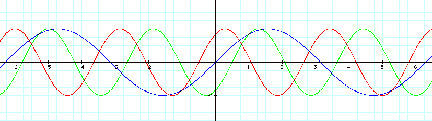
This shows us that phase shift is effected by “b”. Thus, the phase shift is actually “–c/b”.

In summary, given the equation y = a sin (bx +c) the following are true:

· Changes in the value of “a” effects the altitude of the sine graph.

· Changes in the value of “b” effects the period of the graph.

· Changes in the value of “c” in conjunction with the value of “b” together effect the phase shift of the graph.

Return to Matt’s Home Page