Centers
of a triangle
(Assignment 4)
by
J. Matt Tumlin, Cara Haskins, Robin Kirkham, and Venki
Ramachandran
Here we show
that the distance between the Centroid, Circumcenter and the Orthocenter of any
triangle always maintain a constant ratio. HG = 2GC.
We construct
the three centers of the triangle first.
1. The Centroid G
is the intersection of the tree medians of a triangle. The median being a line joining the
midpoint of a side with the opposite vertex.
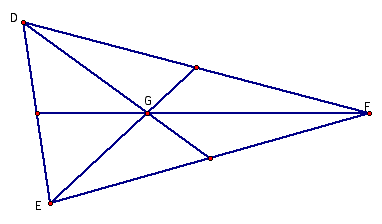
Triangle DEF
has the Centroid at G. Whatever
shape the triangle assumes, G lies within the triangle.
2. The
Orthocenter of a triangle is the point of intersection of the altitudes dropped
from each vertex to the opposite side.
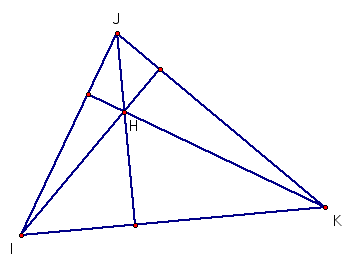
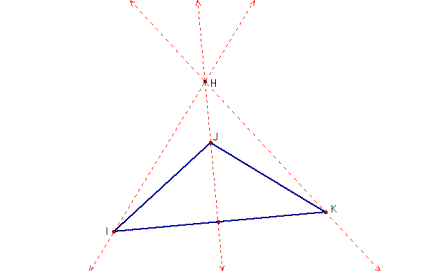
The
orthocenter could be inside or outside the triangle.
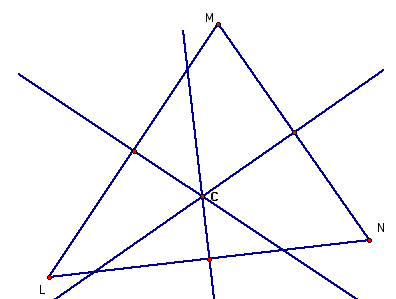
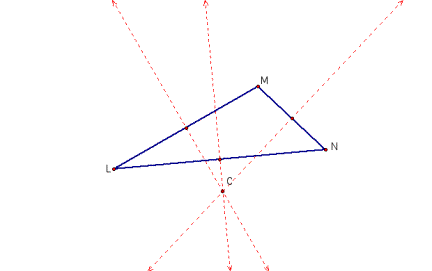
3. The
circumcenter of a triangle is the point of intersection of the perpendicular
bisectors of the sides. A circle
drawn with the circumcenter as the center would pass through the three vertices
of the triangle.
The
circumcenter C of a triangle may lie within or outside of the triangle as
demonstrated above. It can however
be observed that the locus of C will be one of the three perpendicular
bisectors.
3. The INCENTER of a triangle is the point inside the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then I must be on the angle bisector of each angle of the triangle.
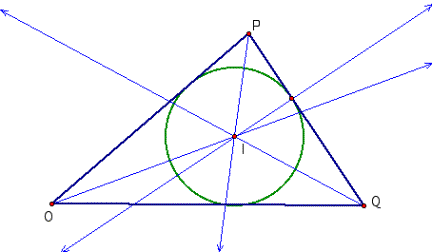
Needless to
say, irrespective of the shape of the triangle, the in-center lies inside the
circle. Further, a circle drawn with
the In-center as a center and radius equal to the perpendicular distance to any
one side will touch the other two sides.
5. To
construct G, H, C and I for a given triangle and observe them
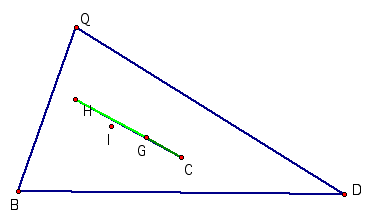
The
circumcenter C, the Centroid G and the Orthocenter are always collinear. When the triangle becomes an
equilateral triangle, all these four points become concurrent. Further, the ratio of the distances
between C, G, and H is constant.
The
circumcenter C, the Centroid G and the Orthocenter are always collinear. When the triangle becomes an
equilateral triangle, all these four points become concurrent. Further, the ratio of the distances
between C, G, and H is constant.
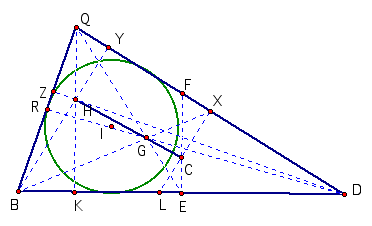
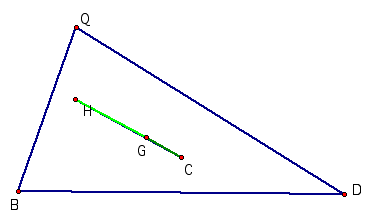
The
Orthocenter, H, is the point of intersection of the perpendiculars BY, DZ, and QK. The Circumcenter, C, is the point of
intersection of EF, RS, and XL. These three lines are the perpendicular
bisectors of the sides QD, BQ, and BD.
The Centroid, G, is the point of intersection of BX, QE, and DR. These
are the lines drawn from the vertex to the midpoint of the sides opposite to
the vertex.
We now need to
prove that the length HG is twice the length of GC.
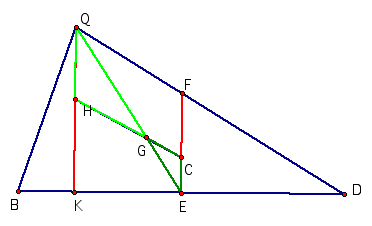
Consider the
two triangles HQG and CGE. These
two triangles are similar. Proof
of this similarity is easily recognized by observing that lines FE and QK are
parallel. Thus angle ECG = angle
QHG. Further, angle CGQ = angle HGE being vertically opposite angles.
Therefore, CG
: GH as QG : GE.
We know that G
being the Centroid of the triangle divides QE in the ration of 1:2. Thus, QG:GE
= 1:2.
Therefore, CG
: GH as 1 : 2.