
Examining
Similar Triangles
(Assignment 6)
by
J. Matt Tumlin, Cara Haskins, and Robin Kirkham
Let us begin our exploration by defining similar figures. In order to prove that any two figures are similar, the measures of corresponding angles must be the same, but the measures of corresponding sides must be multiples (proportional) of each other.
For our
example we are going to construct any triangle ABC:
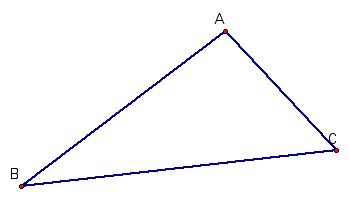
In this
example, let the lengths of the sides of triangle ABC be as
follows:
m BA @ 5 cm
m BC @ 8 cm
m AC @ 4 cm
Let the
measurements of the interior angles of triangle ABC be as
follows:
m angle ABC @ 30 degrees
m angle BAC @ 120 degrees
m angle ACB @ 40 degrees
If we take the
midpoints of this triangle and construct segments from the midpoints to the
vertices, then we can copy these segments to construct a new triangle DEF, as noted
below:
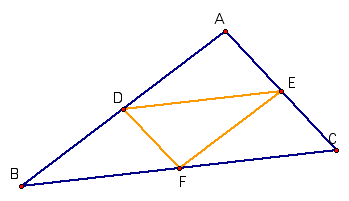
For the new
triangle DEF, the lengths of the sides are as follows:
m FE @ 3 cm
m DE @ 6 cm
m DF @ 2 cm
The
corresponding angles are congruent.
Therefore,
these two triangles constructed from one triangle are similar, as the sides are
in proportion and the angles are congruent.