

1. Construct circle AB.
2. Construct chord BC.
3. Construct the midpoint D of the chord.
4. Construct a line through point D perpendicular to BC. This line is the perpendicular bisector of the chord.
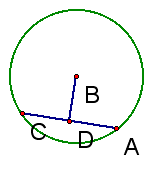
5. Drag point C around the circle and observe the perpendicular bisector.
Write a conjecture about the perpendicular bisector of any chord in a circle.
6. Hide the perpendicular bisector and construct AD.
7. Measure the length of AD. This is the distance from the chord to the center.
8. Measure the length of BC.
9. Drag point C around the circle and observe the measures.
How is the length of the chord related to its distance from the center?
10. You can make a graph that shows this relationship: Select the length of BC and the length of AD, in that order; then, in the Graph menu, choose Plot As (x,y). You should get axes and a point G whose coordinates are the measures you selected.
11. Drag point C to see how it controls point G.
12. To graph all the possible locations for point G, select it and point C; then, in the Construct menu, choose Locus.
13. Drag point C to see point G travel along the locus. Click Here.
14. Drag point A or point B to see what effect changing the circle's radius has on the graph.
Write a paragraph describing the graph. Answer these questions in your paragraph: Look at the value of y where the locus intersects the y-axis. What does this value represent in the circle? Look at the value of x where the locus intersects the x-axis. What does this value represent in the circle? As point G moves from left to right, what happens to the value of its y-coordinate? What does this have to do with what's happening to the chord?
15. Construct HI, another chord on the circle.
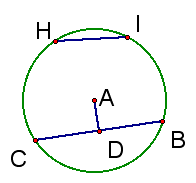
16. Measure HI.
17. Measure the distance from HI to the center of the circle.
18. Drag point H or point I and watch the length measure. Try to make this length of BC as you can. Click Here.
Write a conjecture about congruent chords in a circle.