

1. Construct segment AB.
2. Construct circle A with radius AB.
3. Construct secant BC, making sure point C fall on the circle.
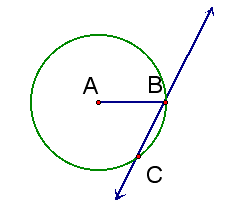
4. Measure angle ABC.
5. Drag point C around the circle and observe the angle measure. Click Here
What happens to the measurement of angle ABC as point C gets closer to point B? What's the measure of angle ABC when point C is right on top of point B?
When points B and C coincide, your line intersects the circle in a single point, so it's tangent to the circle. How is a tangent related to the radius at the point of tangency?
Use what you observed above to construct a line in your sketch that is always tangent to the circle. Describe how you did it.
Come up with methods for constructing two circles that always intersect in one point. The circles could be internally tangent (one inside the other) or externally tangent (neither inside the other).