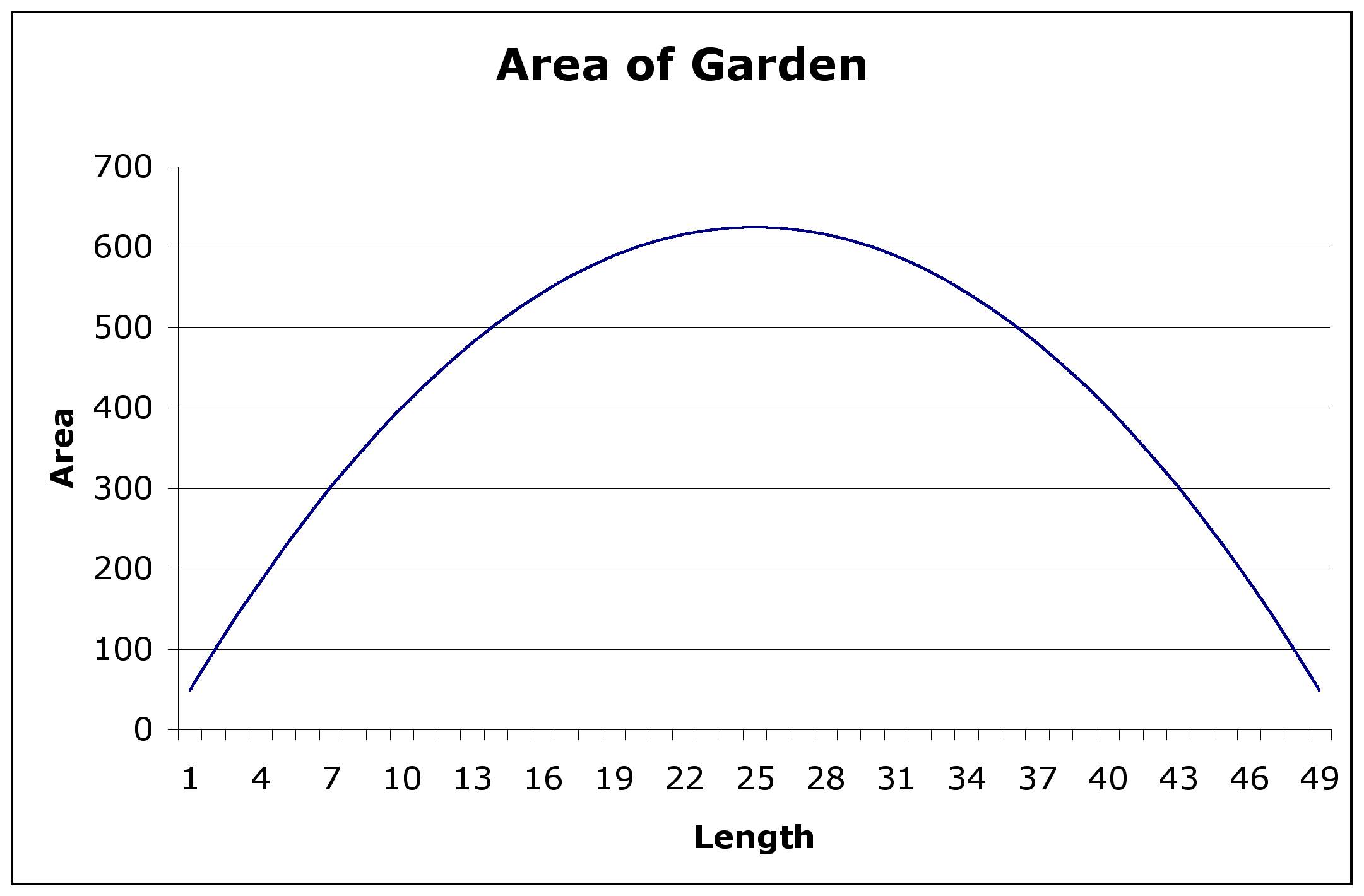
The goal of the problem is to maximize the area. In order to accomplish this, we first need to look at how the area is formed based on the dimensions. Assuming the garden is rectangular, area = length x width. We can use a spreadsheet to calculate all possible dimensions for a rectangle that has a perimeter equal to 100 meters.
| Length | Width | Area |
| 1 | 49 | 49 |
| 2 | 48 | 96 |
| 3 | 47 | 141 |
| 4 | 46 | 184 |
| 5 | 45 | 225 |
| 6 | 44 | 264 |
| 7 | 43 | 301 |
| 8 | 42 | 336 |
| 9 | 41 | 369 |
| 10 | 40 | 400 |
| 11 | 39 | 429 |
| 12 | 38 | 456 |
| 13 | 37 | 481 |
| 14 | 36 | 504 |
| 15 | 35 | 525 |
| 16 | 34 | 544 |
| 17 | 33 | 561 |
| 18 | 32 | 576 |
| 19 | 31 | 589 |
| 20 | 30 | 600 |
| 21 | 29 | 609 |
| 22 | 28 | 616 |
| 23 | 27 | 621 |
| 24 | 26 | 624 |
| 25 | 25 | 625 |
| 26 | 24 | 624 |
| 27 | 23 | 621 |
| 28 | 22 | 616 |
| 29 | 21 | 609 |
| 30 | 20 | 600 |
| 31 | 19 | 589 |
| 32 | 18 | 576 |
| 33 | 17 | 561 |
| 34 | 16 | 544 |
| 35 | 15 | 525 |
| 36 | 14 | 504 |
| 37 | 13 | 481 |
| 38 | 12 | 456 |
| 39 | 11 | 429 |
| 40 | 10 | 400 |
| 41 | 9 | 369 |
| 42 | 8 | 336 |
| 43 | 7 | 301 |
| 44 | 6 | 264 |
| 45 | 5 | 225 |
| 46 | 4 | 184 |
| 47 | 3 | 141 |
| 48 | 2 | 96 |
| 49 | 1 | 49 |