

Conics Instructional Unit
Day 6 - Circles
by
Mandy Stein
Circle
The locus of all points equal distance from a fixed point, called the center
Standard Equation of a Circle
With center (h , k)
(x – h) 2 + (y - k) 2 = r2

To graph a circle:
(x – 2) 2 + y2 = 16
Center: (2,0)
Radius: ![]() = 4
= 4
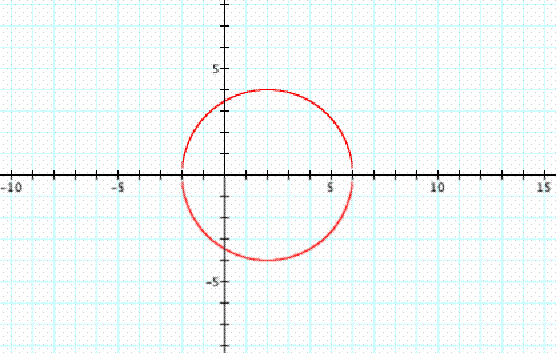
(x – 4)2 + (y + 3) 2 = 25
Center: (4,-3)
Radius: ![]() = 5
= 5

To graph an equation not in standard form:
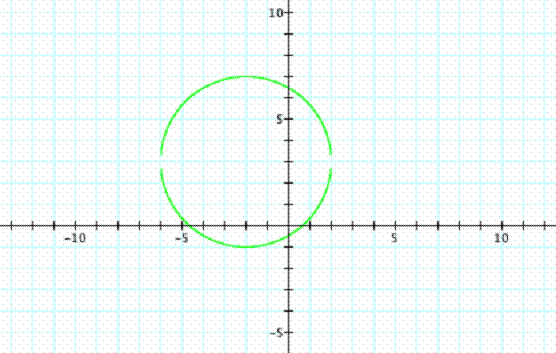
x2 + y2 + 4x – 6y – 3 = 0
First, we put the equation in standard form by completing the square
x2 + y2 + 4x – 6y = 3
(x2 + 4x + 4) + (y2 – 6y + 9) = 3 + 4 + 9
(x + 2) 2 + (y – 3) 2 = 16
Center: (-2,3)
Radius: ![]() = 4
= 4
To write the equation of a circle:

Center: (4, 2)
Radius: 3
(x - 4) 2 + (y – 2) 2 = 9
Determine if the point (1,5) is inside, on, or outside the circle given by the equation (x – 2) 2 + (y +1) 2 = 9
To solve this problem, first determine the radius of the circle. The radius is the square root of 9, which equals 3. We also determine the center of the circle, which is (2, -1). Then we determine how far (1,5) is from the center using the distance formula
d =
![]()
The distance between the center of the circle and the point
(1,5) is ![]() . Since this is larger than 3 (the radius of the circle) the
point is outside the circle.
. Since this is larger than 3 (the radius of the circle) the
point is outside the circle.
Day 7 - Introduction to Hyperbolas