

Conics Instructional Unit
Day 3 - Parabolas
by
Mandy Stein
Parabola
The locus of all points P(x,y) equidistant from a fixed point, called the focus, and a fixed line, called the directrix.
Axis of symmetry – passes through the vertex and divides the parabola into two symmetric parts.
Vertex – the midpoint between the focus and directrix.
Standard Equation of a Parabola
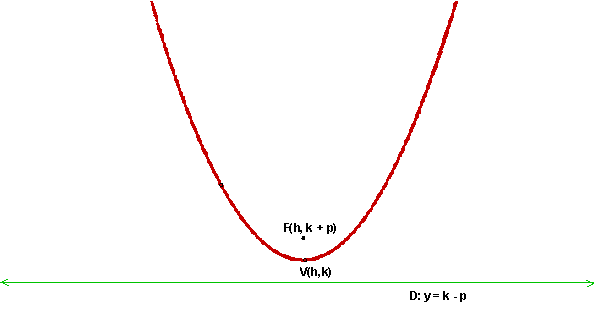
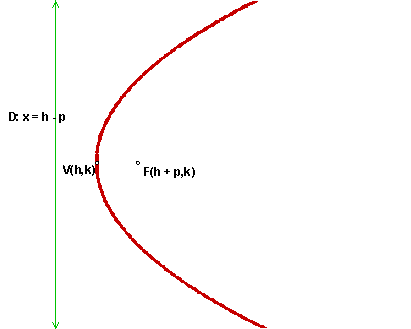
Standard equation of a parabola with its vertex at (h,k)
|
Horizontal Directrix y -
k =
p > 0 opens up p < 0 opens down Focus: (h, k + p) Directrix: y = k – p Axis of symmetry: x = h
|
Vertical Directrix x -
h =
p > 0 opens right p < 0 opens left Focus: (h + p, k) Directrix: x = h - p Axis of symmetry: y = k
|
Horizontal Directrix
Vertical Directrix
To graph a parabola:
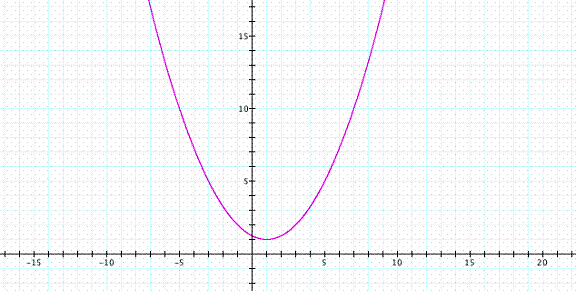
º > 0 so the parabola opens up
Vertex: (1,1)
Focus: (1,2)
Directrix: y = 0
Axis of symmetry: x = 1
x – 3 = -
![]() (y + 1) 2
(y + 1) 2
-![]() < 0 so the parabola opens down
< 0 so the parabola opens down
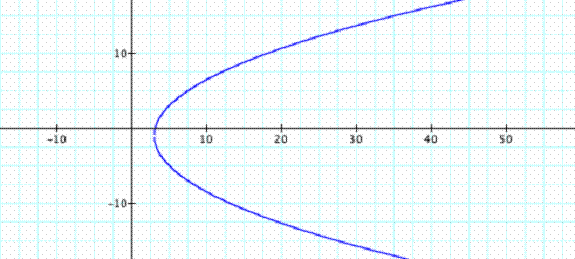
Vertex: (3,-1)
Focus: (1,-1)
Directrix: x = 5
Axis of symmetry: y = -1
y + 3 =
![]() x2
x2
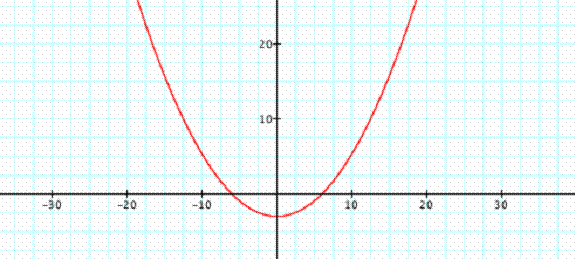
![]() > 0 so the parabola opens up
> 0 so the parabola opens up
Vertex: (0,-3)
Focus: (0,0)
Directrix: y = -6
Axis of symmetry: x = 0
To graph a parabola not in standard form:
y2 – 8y + 8x + 8 = 0
First, we put the equation in standard form by completing the square
y2 – 8y = -8x – 8
y2 – 8y + (-4) 2 = -8x – 8 +(-4)2
(y – 4)2 = -8x + 8
(y – 4)2 = -8(x – 1)
-![]() (y – 4)2 = x – 1
(y – 4)2 = x – 1
x – 1 = -![]() (y – 4)2
(y – 4)2
Vertical Directrix
-![]() < 0 so the parabola opens down
< 0 so the parabola opens down
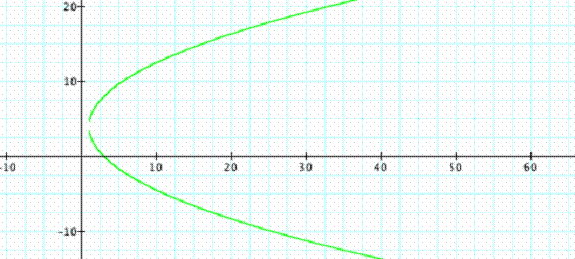
Vertex: (1,4)
Focus: (-1,4)
Directrix: x = 3
Axis of symmetry: y = 4
To write the equation of a parabola:
Horizontal directrix
y - k
= ![]() ( x – h)2
( x – h)2
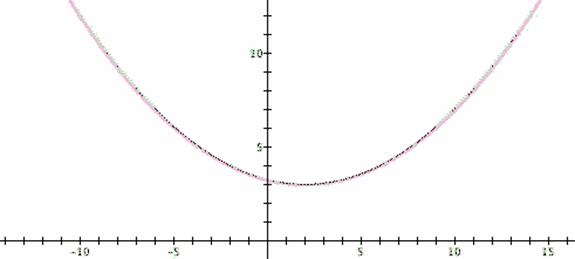
Vertex: (2, 3)
Focus: (2, 7)
Directrix: y = -1
h = 2, k = 3, p = 4
y – 3 =
![]() ( x – 2)2
( x – 2)2
Vertical directrix
x - h
= ![]() (y – k)2
(y – k)2
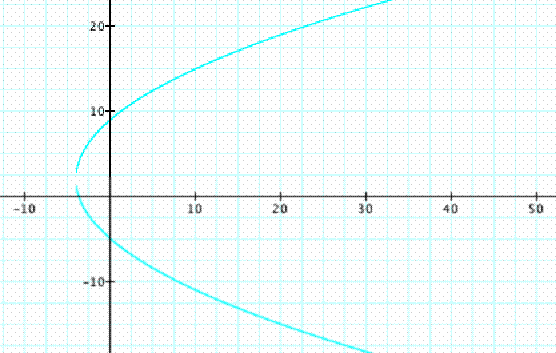
Vertex: (-4, 2)
Focus: (-1, 2)
Directrix: x = -7
h = -4, k = 2, p = 3
x + 4 =
![]() ( y – 2)2
( y – 2)2
Day 4 - Introduction to Ellipses