

Conics Instructional Unit
Day 10 - Summary
by
Mandy Stein
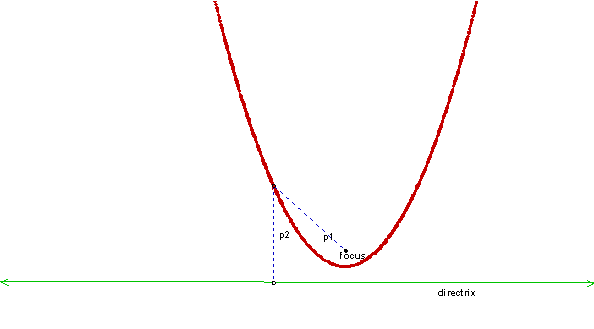
Standard Equation of a Parabola
Standard equation of a parabola with its vertex at (h , k)
|
Horizontal Directrix y =
p > 0 opens up p < 0 opens down Focus: (h, k + p) Directrix: y = k – p Axis of symmetry: x = h
|
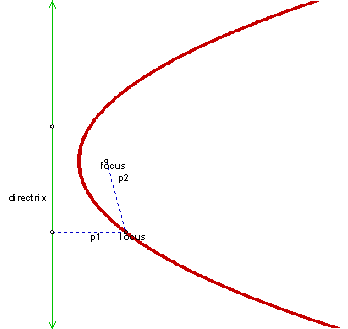
Vertical Directrix x - h =
p > 0 opens right p < 0 opens left Focus: (h + p, k) Directrix: x = h - p Axis of symmetry: y = k
|
Standard Equation of an Ellipse
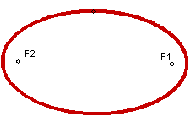
Standard equation of an ellipse centered at (h , k)
|
Horizontal Major Axis
Vertices: (h – a, k) & (h + a, k) Co-Vertices: (h, k + b) & (h, k – b) Foci: (h – c, k) & (h + c, k) Major axis = 2a Minor axis = 2b a2 > b2 a2 - b2 = c2 |
Vertical Major Axis
Vertices: (h, k – a) & (h, k + a) Co-Vertices: (h – b, k) & (h + b, k) Foci: (h, k – c) & (h, k + c) Major axis = 2a Minor axis = 2b a2 > b2 a2 - b2 = c2 |

Standard Equation of a Circle
With center (h , k)
(x – h) 2 + (y - k) 2 = r2

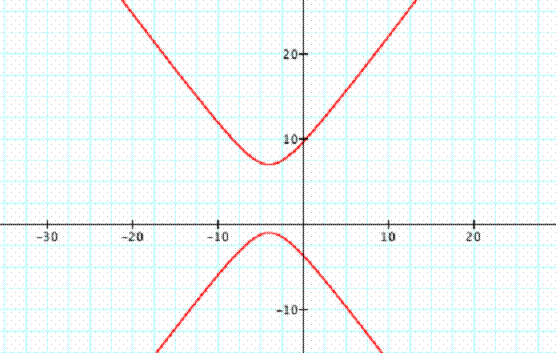
Standard Equation of a Hyperbola
Standard equation of an hyperbola centered at (h , k)
|
Horizontal Transverse Axis
Vertices: (h – a, k) & (h + a, k) Co-Vertices: (h, k + b) & (h, k – b) Foci: (h – c, k) & (h + c, k) Slope of
asymptote = + Transverse axis = 2a Conjugate axis = 2b a2 + b2 = c2 |
Vertical Transverse Axis
Vertices: (h, k – a) & (h, k + a) Co-Vertices: (h – b, k) & (h + b, k) Foci: (h, k – c) & (h, k + c) Slope of
asymptote = + Transverse axis = 2a Conjugate axis = 2b a2 + b2 = c2 |
Determining the different shapes by the equation:
Parabola: only the x or the y is squared, not both
Circle: x2 and y2 have the same coefficient with the same sign
Ellipse: x2 and y2 have difference coefficients with the same sign
Hyperbola: x2 and y2 have difference coefficients and different signs
Examples:
x2 + 2x + y2 + 6y = 15 would be a circle
4y2 – 8y – x2 – 4x – 4 = 0 would be a hyperbola
4x2 + 9y2 - 8x – 18y – 23 = 0 would be an ellipse
x2 – 8x + y = -2 would be a parabola