

Contextual Teaching and Learning Essay
Linear Programming
By
Mandy Stein
Linear programming is used to maximize profit or minimize costs in a variety of industries.
There are several components of linear programming:
Constraints - These are represented in the form of inequalities. They represent limitations on materials, resources, or time.
Feasible Region - The solution set of the system of constraints.
Objective Function - The function to be minimized or maximized. This function represents profit or cost.
Corner-Point Principle - The maximum and minimum values of an objective function occur at one of the vertices of the feasible region.
Problem:
A farmer has 90 acres on which to plant millet and alfalfa. Seed for one acre of millet costs $4 and seed for one acre of alfalfa costs $6. Labor costs for millet are $20 per acre and labor costs for alfalfa are $10 per acre. The expected income for an acre of millet is $110 and the expected income for an acre of alfalfa is $150. The farmer wants to spend no more than $480 for seed and $1400 for labor. What should he plant to maximize his profit?
The objective function represents the profit the farmer will make from planting m acres of millet and a acres of alfalfa.
R = 110m + 150a
What the farmer plants is limited by these constraints:
Translating these constraints into inequalities gives us the following system of inequalities:
m + a < 90
4m + 6a < 480
20m + 10a < 1400
0 < m
0 < a
Next, we will graph the system of constraints to obtain the feasible region and locate the vertices. Note: The last two inequalities were added because a negative number of acres cannot be planted.
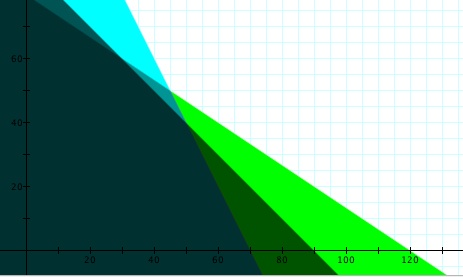
Based on the Corner-Point Principle, the maximum value will be located at one of the vertices. Thus, we evaluate the objective function at each vertex to determine which combination produces the maximum profit.
|
Vertex (m,a) |
Objective Function |
|
(0,80) |
R = 110(0) + 150(80) = 12000 |
|
(30,60) |
R = 110(30) + 150(60) = 12300 |
|
(50,40) |
R = 110(50) + 150(40) = 11500 |
|
(70,0) |
R = 110(70) + 150(0) = 7700 |
We can see from the table that income is maximized when 30 acres of millet and 60 acres of alfalfa are planted. The maximum income is $12,300.