

Problem 3.
The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. Note: C may be outside of the triangle.
Construct the circumcenter C and explore its location for various shapes of triangles. It is the center of the circumcircle (the circumscribed circle) of the triangle.
The first case we will look at is an equilateral triangle.

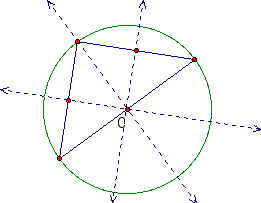
Here we notice the circumcenter is inside the triangle and the circumscribed circle touches all three vertices of the triangle. We also notice that all of the perpendicular bisectors pass through the vertices of the triangle.
Next, we will look at acute triangles that are not equilateral.
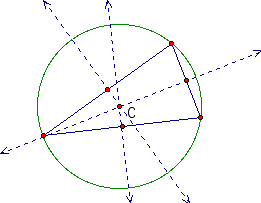

Looking at these pictures we notice both are similar to the equilateral triangle. The circumcenter is still inside the triangle and the circle touches all three vertices of the triangle. However, we notice that the perpendicular bisectors do not intersect the vertices of the triangles.
Next, we will look at right triangles.
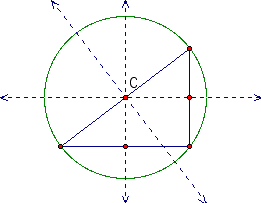
Looking at these pictures we notice that the circumcenter is located on one of the sides of the triangle. None of the perpendicular bisectors intersect the vertices.
Next, we will look at isosceles right triangles.

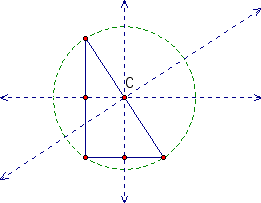
Looking at these pictures we notice that C is still on one of the sides of triangle and that one of the perpendicular bisectors intersects a vertex in the triangle.
Next, we will look at obtuse triangles.


Looking at these pictures we notice that C is now outside the triangle. None of the perpendicular bisectors intersects the vertices of the triangle, but one of the perpendicular bisectors is close to intersecting a vertex in the first picture. It also appears that as the obtuse angle increases, the circumcircle gets larger.
Let's look at a few more triangles to investigate those things.
First, let's look at a couple of obtuse isosceles triangles.


Looking at the pictures of the obtuse isosceles triangles. We notice that C is outside the triangle and that one of the perpendicular bisectors intersects a vertex in the triangle.
Now, let's look at a few more isosceles triangles.

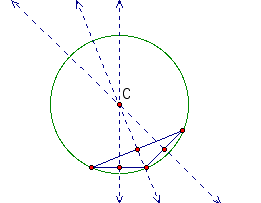
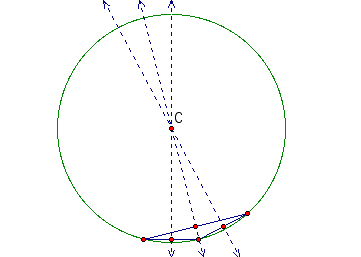
These graphs confirm that as the obtuse angle gets larger, the circle gets larger as well.
Putting all of this information together there are several
things we have learned about circumcenters of triangles and circumcircles
of triangles. The circumcircle always intersects all the vertices
of a triangle. The circumcircle of an obtuse triangle gets larger
as the obtuse angle increases. The circumcenter of an acute (including
equilateral) triangle is inside the triangle. The circumcenter
of a right triangle is on one of the sides of the triangle. The
circumcenter of an obtuse triangle is outside the triangle. The
perpendicular bisectors of an equilateral triangle intersect all
three vertices. If a right triangle is isosceles one of the perpendicular
bisectors intersects one of the vertices of the triangle, otherwise,
the perpendicular bisectors of a right triangle do not intersect
the vertices. If an obtuse triangle is isosceles one of the perpendicular
bisectors intersects one of the vertices, otherwise the perpendicular
bisectors of an obtuse triangle do not intersect the vertices.
From the last two observations we can conclude that the one of
the perpendicular bisectors of an isosceles triangle will intersect
one of the vertices.