

Statement: The medians of a triangle are concurrent, and the point of concurrence, the centroid, is two-thirds the distance from each vertex to the opposite side.
Proof:
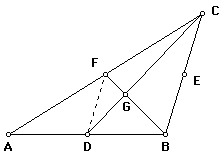
1. Points A, F, and C are distinct and collinear. F is the midpoint
of segment(AC). Since the sum of the angles of triangle ABC is
180 degrees, m(ABC) < 180. That F is between A and C implies
that 0 < m(ABF) < m(ABC). F is not B; therefore, segment(BF)
intersects segment(AC). [Betweenness Axiom] Now, A, D, and B are
distinct and collinear, and D is the midpoint of segment(AB).
Thus, m(DBF) = m(ABF) and m(DBC) = m(ABC). So, 0 < m(DBF) <
m(DBC), and segment(BF) intersects segment(CD). Let point G be
the intersection of BF and CD. Therefore, G is a point on segment(BF).
2. Similarly, points B, E, and C are distinct and collinear; E
is the midpoint of segment(BC); and m(CAB) < 180. That E is
between B and C implies that 0 < m(CAE) < m(CAB). E is not
A; therefore, segment(AE) intersects segment(BC). Since F is the
midpoint of segment(FA), m(FAE) = m(CAE) and m(FAB) = m(CAB).
So, 0 < m(FAE) < m(FAB), and segment(AE) intersects segment(FB).
Let point H be the intersection of AE and FB. Therefore, H is
a point on segment(FB).
3. The opposite angles formed at the intersection of BF and CD
are equal. That is, m(FGC) = m(BGD) and m(DGF) = m(CGB). If we
join points F and D, ADF is formed which is similar to ABC. [d(AC)
= 2(d(AF)), d(AB) = 2(d(AD)), and m(CAB) = m(FAD).] Thus, d(BC)
= 2(d(DF)). Now, the segment joining the midpoints of two sides
of a triangle is parallel to that triangle's third side. Since
segment(BF) is a transversal of parallel segments DF and BC, alternate
interior angles GFD and GBC are equal. Thus, by the Angle-Angle
Theorem, FDG is similar to BCG. As before, the constant of proportionality
is 2; so, d(BG) = 2(d(FG)).
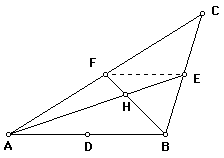
4. The opposite angles formed at the intersection of FB and AE
are equal. That is, m(AHF) = m(EHB) and m(FHE) = m(BHA). If we
join points F and E, FEC is formed which is similar to ABC. [d(CA)
= 2(d(CF)), d(CB) = 2(d(CE)), and m(BCA) = m(ECF).] Thus, d(AB)
= 2(d(FE)). The segment joining the midpoints of two sides of
a triangle is parallel to that triangle's third side. Since segment(FB)
is a transversal of parallel segments FE and AB, alternate interior
angles HFE and HBA are equal. Thus, by the Angle-Angle Theorem,
EFH is similar to ABH. The constant of proportionality is 2; so,
d(BH) = 2(d(FH)).
5. By the Existence Axiom, for points B and F there exists a unique
line containing B and F. It has been shown that points G and H
are on segment(BF). Further, it has been shown that d(BG) = 2(d(FG))
and d(BH) = 2(d(FH)). In addition, both G and H are between B
and F. Therefore, G and H are one-and-the-same point. So, the
three medians of ABC are concurrent.
6. In a similar manner, it can be shown that d(CG) = 2(d(DG))
and d(AH) = 2(d(EH)). Therefore, the centroid, G, is two-thirds
the distance from each vertex to the opposite side.