

Description: For any triangle ABC, construct lines through an arbitrary point P such that the lines are perpendicular to the sides of triangle ABC. The point of intersection of the perpendiculars and the sides of the triangle are the vertices of a new triangle RST, the pedal triangle for the pedal point P.
Characteristics of the pedal point and pedal triangle for various positions of P:
When P is the circumcenter of triangle ABC, the pedal triangle is the medial triangle.
When P is the orthocenter of triangle ABC, the pedal triangle is the orthic triangle.
When P is on a side of triangle ABC, the pedal point is a vertex of the pedal triangle.
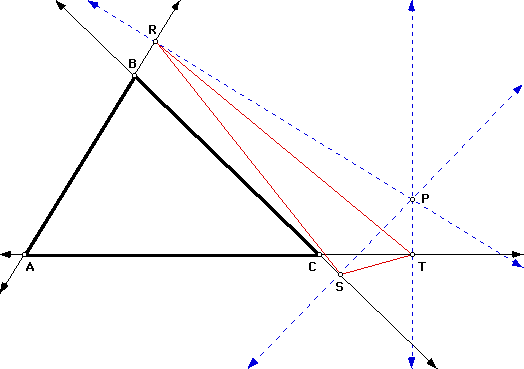
When P is a vertex of triangle ABC, the pedal triangle is degenerate. Triangle RST is an altitude of triangle ABC.
Click here to access a GSP sketch on which you can move point P to these positions.
The vertices of the pedal triangle are collinear when the pedal point lies on the circumcircle of triangle ABC. The line segment thus formed is a segment of the Simpson Line. Click here to view an animation of P around the circumcircle. Note that, when the pedal point P lies on the ray from the vertex of triangle ABC through the circumcenter, the degenerate pedal triangle is the side of the triangle ABC subtended by the angle at that vertex. In addition, the degenerate pedal triangle bisects the segment whose endpoints are the pedal point and the orthocenter.
The envelope of the Simpson Line as the pedal point is moved along the circumcircle of triangle ABC is a deltoid. Click here to view the creation of this envelope as P moves around the circumcircle.
Consider the case when P lies on the incircle of triangle ABC. When P is the point of intersection of a side of triangle ABC and the incircle (i.e., a tangent point), P is a vertex of the pedal triangle. The loci of the midpoints of the sides of the pedal triangle RST are three ellipses. Click here and the animate button to view these loci.
When ABC is a right triangle, the loci of the midpoints of the sides of the pedal triangle are two ellipses and a circle tangent to the two perpendicular sides of triangle ABC. The center of this circle is the midpoint of the segment joining the incenter and the vertex at the right angle. Click here and the animate button to view these loci.
We now construct an excircle of triangle ABC which is tangent to segment BC and the extensions of segments AB and CA. When we trace the loci of the midpoints of the sides of the pedal triangle, we observe that three ellipses are formed. The foci of one ellipse lie on the bisector of angle CAB. These points are the center of the excircle and the intersection of the excircle and the angle bisector. The segments which join the foci of each of the other two ellipses are, themselves, bisected by a bisector of an exterior angle of triangle ABC (i.e., ray(BO) or ray(CO)). Click here to view these loci and the described relations.