

A parametric curve in the plane is a pair of functions
where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve.
The most simple case involving sines and cosines would be the parametric curve
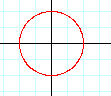
This graph is the one of the well known unit circle. The center of this circle is at (0,0). We will take a look at this graph and then how changing some values within the equation changes the graph.
What about the case where
x = cos(t) + a , y = sin(t) + b OR x = cos(t) - a , y = sin (t) - b for the same t as above and different a's
.
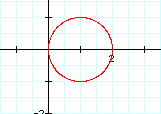
|
|
|
|
|
|
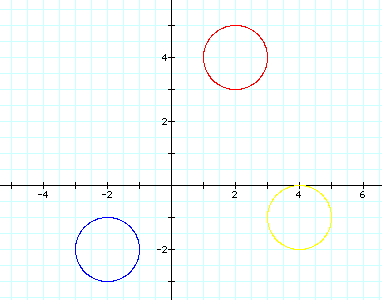
When 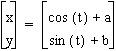 , The
graph is a circle with center at (a, b) and radius 1.
, The
graph is a circle with center at (a, b) and radius 1.
Let's look at the case when 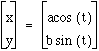 .
.
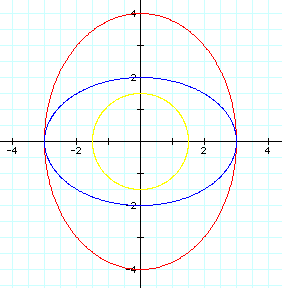
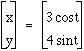 , Blue Curve =
, Blue Curve = 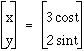 , and
, and 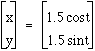 .
.When a and b change in the equation, we get some unique graphs. When a< b, the curve is an ellipse with the minor axis on the x-axis. This is the case in the red ellipse. When a = b, the curve is a circle. The major and minor axes have the same length. This is the case in the yellow curve. When a>b, the curve is an ellipse with the minor axis on the y-axis and the major axis on the x-axis. This is the case in the blue ellipse. A and B tell us 1/2 the length of the major and minor axis.
More Explorations:
For some interesting graphs, go to a Graphing Calculator program and try graphing some equations such as
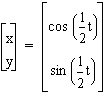 ,
, 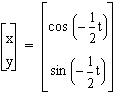 ,
or
,
or 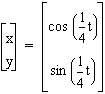 .
.
Which of these do you think would produce the following graph?
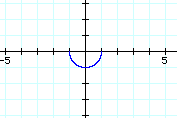
Return to April's home page