

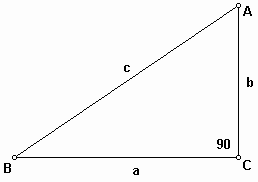
In a right triangle, the side opposite the
right angle is called the hypotenuse. The other two sides are
called legs. If ![]() and
and ![]() are
the lengths of the legs and
are
the lengths of the legs and ![]() is the length of
the hypotenuse, then
is the length of
the hypotenuse, then
which is called the Pythagorean theorem.
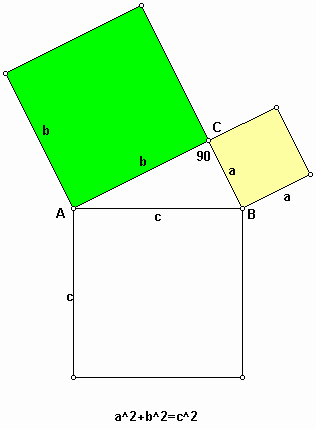
This was discovered on a Babylonian tablet circa 1900-1600 BC Whether Pythagoras (c. 560-c. 480 BC.) or someone else from his School was the first to discover its proof can't be claimed with any degree of credibility.
Here, I would like to show several proofs of Pythagorean theorem.
Proof 1. (Euclid's proof)
You, first of all, should know the following properties:
Now, we are ready to prove.
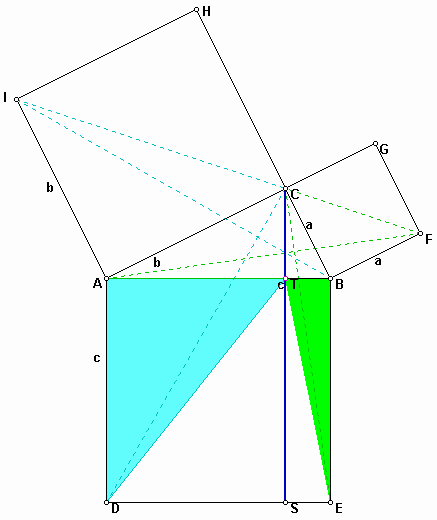
First, draw the perpendicular line from the point C to the side DE.
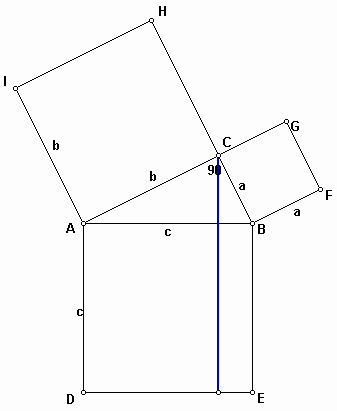
In suqare ACHI, construct a triangle ACI. From the second and third properties, we have a triangle ABI which has the same area as the triangle ACI.
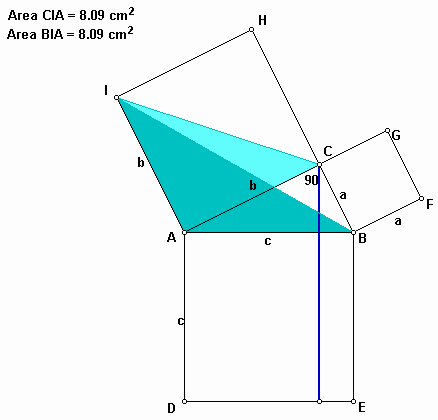
Similarly, we have two triangles BFC and BFA which have the same area in the square BFGC.
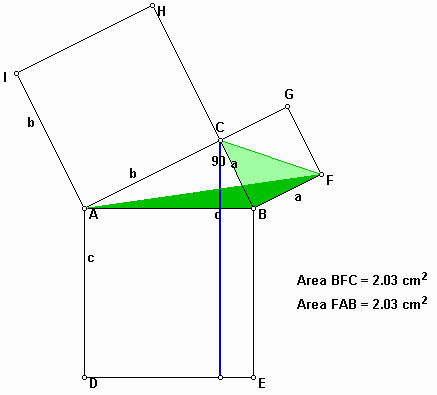
Now, shear the triangle ABI whose area is the half of the area of the square ACHI, then you obtain a triangle ACD and a triangle ADT whose area is the same as the one of ADC again.
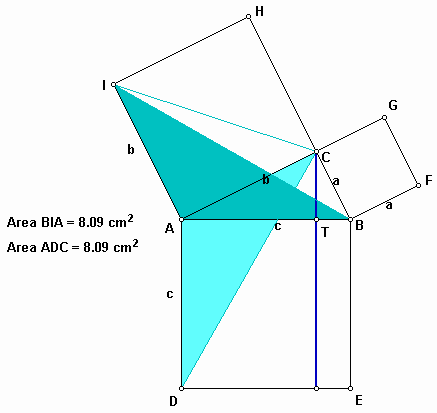
Again, using the properties given above, we have another triangle ADT having the same area.
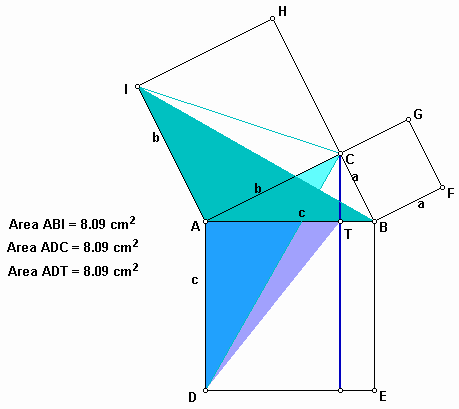
You already know the area of a triangle ADT is half of the rectangle ADST. Similarly, you get triangles in the square BFGC as follows:
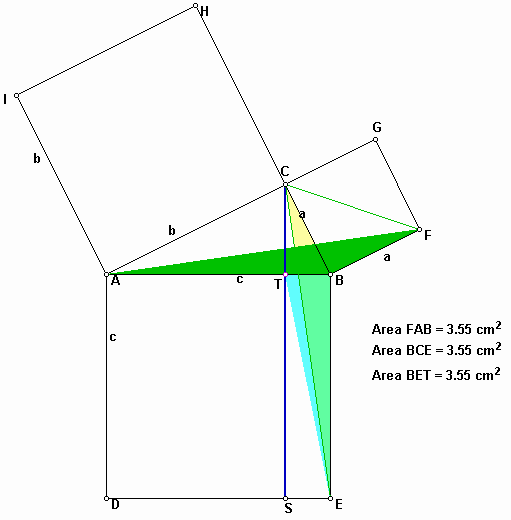
Since triangle ADT is half area of the rectangle ADST and BET is half of BEST, the sum of the areas of ACHI and BFGC equals to the area of the square ADEB. As a result, we have
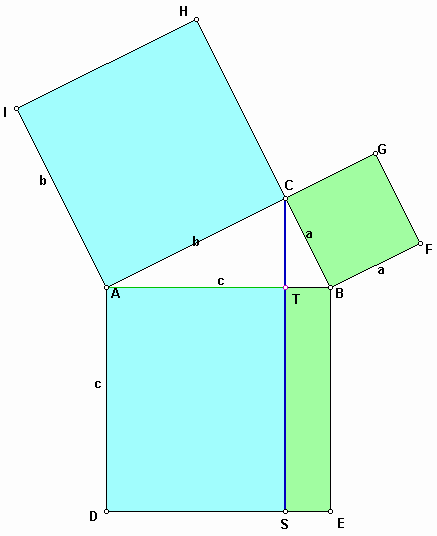
It gives
Proof 2. (Dissection proof)
We have a right triangle ABC,
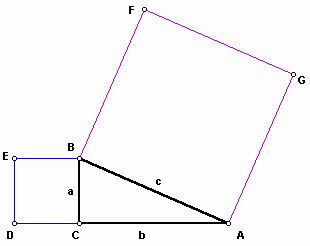
Translate the square BCDE horizontally until its left edge bisects the hypotenuse.
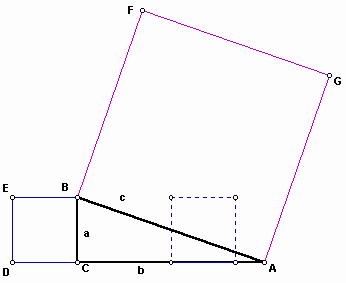
Then translate the dotted square vertically until it is centered on the square ABFG of side c.
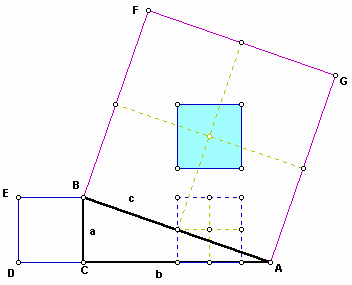
If we cut to make out to the edges form four quadrilateral pieces, the four quadrilateral pieces can be rearranged to fill the square of side b exactly. From the follwing figure, we can show that each of the two outer edges of the quadrilateral pieces has length
![]() .
.
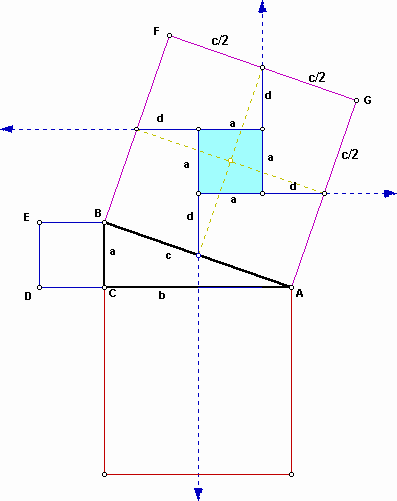
The lengths of the quadrilateral pieces can be written in terms of a, c, and d, and as a result, the area of a quadrilateral piece can be expressed in terms of a, c, and d.
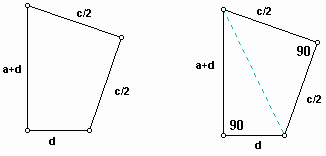
The area
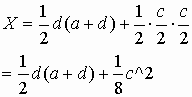
And
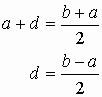
This gives
We already know that
Thus
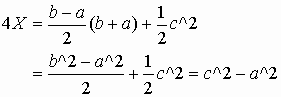
Now we have
Proof 3. (Algebraic proof)
Let the sides of a right triangle a, b, and c which is the hypotenuse. We are going to use the properties of similarity of triangles. In the right triangle ABC, as you can notice in the following triangle, there exist two right triangles, ACD and CBD.
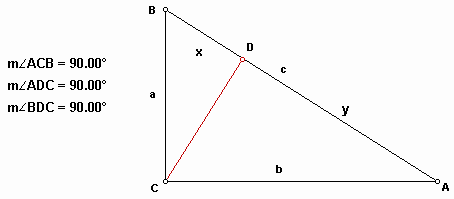
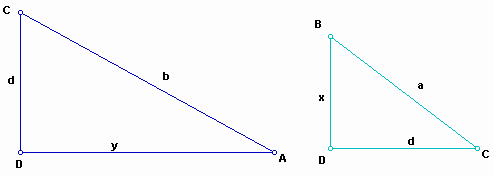
The properties of similarity gives us
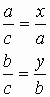
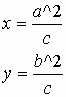
Thus,
Moreover, three integers a, b, and c that satisfy the Pythagorean theorem are called Pythagorean Triples. In fact, there are infinitely many such numbers and exits a way to generate all the triples.