
Observations Made by the Author, Sarah Mason

Whenever we are given two circles and are asked to find the circle tangent to both, we must create a locus of the center of this new circle. This locus will be an ellipse with foci at the centers of the two given circles.
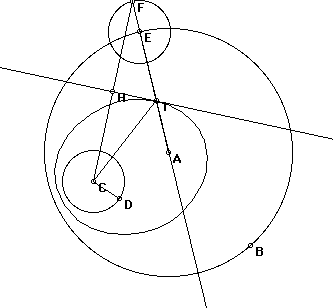
To determine a tangent circle, we can select any point at random (on the diagram below, this is point R) from this ellipse to be our center. If we construct a line from R to each center (C and A) we can determine where the point of tangency occurs. This also shows us the length of the radius and therefore allows us to construct the circle.
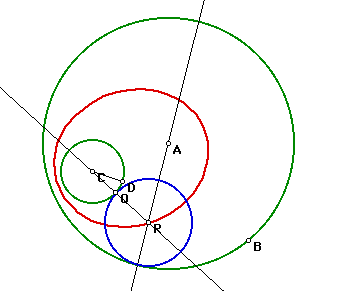
It can also be observed that,
because of this locus of centers, an infinite number of circles
exist which are tangent to two given circles.
For two given circles with a point of tangency on one of the circles, several cases exist.
Let's first look at what happens when the point is located on the larger circle.
Case 1: The larger and smaller circles do not interesct.
Subcase a: When the smaller circle is interior to the larger circle, one tangent circle exists and this is located inside the larger circle.
Subcase b: When the smaller circle is exterior to the larger circle,only one tangent circle exists, but it is located outside the larger circle.
Case 2: The larger and smaller circles do intersect.
Two tangent circles exist, one exterior to and one interior to the larger circle. Both of these circles are exterior to the small circle unless the point of tangency is located on the interior of the smaller circle.
Now let's look at what happens when the point is located on the smaller circle.
Case 1: The larger and smaller circles do not intersect.
Subcase a: When the smaller circle is interior to the larger circle, two tangent circles exist. The smaller circle is interior to one of these and exterior to the other.
Subcase b: When the smaller circle is external to the larger circle, only one tangent circle exists, and it is exterior to both.
Case 2: The larger and smaller circles intersect.
Two tangent circles exist, one interior to the smaller circle and one exterior to the smaller circle. Both of these are exterior to the larger circle if the designated point is exterior to it, and interior to it if the designated point is interior to the the larger circle.