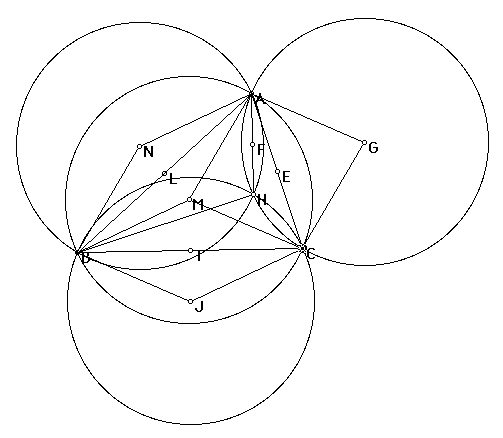---

The Circumcenters of the four triangles form parallelograms when connected to certain vertices

To investigate this conjecture, we need to examine one of the circumcenters and the vertices it is connected to during this phenomena.

Let's look at the points A, N, B, and M. M is the circumcenter of triangle ABC and N is the circumcenter of triangle AHB. By the definition of circle, AN=BN and MB=MA. By proofs found on the previous two links, we know that the radii of the circumcircles are equal. This means that all four sides of parallelogram BNAM are equal, and it is therefore a rhombus. By the definition of rhombus, AN is parallel to MB and NB is parallel to AM. So, by the defintion of parallelogram, AMBN is a parallelogram. This holds true also for AGCM and BMGJ.