Assignment #1
Nicole Mosteller
EMAT 6680

During my investigation, I noticed that the relation above made a dramatic change when the values of a and b are both equal to 1. This dramatic change in the graph prompted me to investigate other values of a = b.

Figure 1: a and b equal to 1.

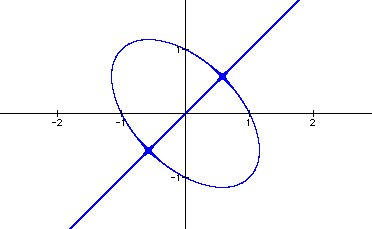
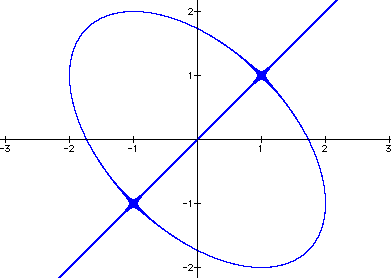
In both Figure 1 and Figure 2, the graphs resemble the composition of an ellipse and the line y=x. Notice as the value of a and b become larger, the ellipse grows larger proportionally.

Figure 2: a and b equal to 3.

Question #2 of Investigation #1 addresses the composition of two relation equations. Within this question, we notice that when two relation equations are multiplied (i.e., f(x)*g(x)), the resulting relation equation's graph is the two original relations. Since our graph has both an ellipse and a straight line, the two original equations must be of an ellipse and a straight line. Now the question becomes how do we transform the equation

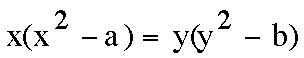
so that we have the equations for both an ellipse and a straight line? To simplify matters, remember Below are the steps that were taken to transform the equation (Shout-out to Jadonna Brewton - Thanks!)

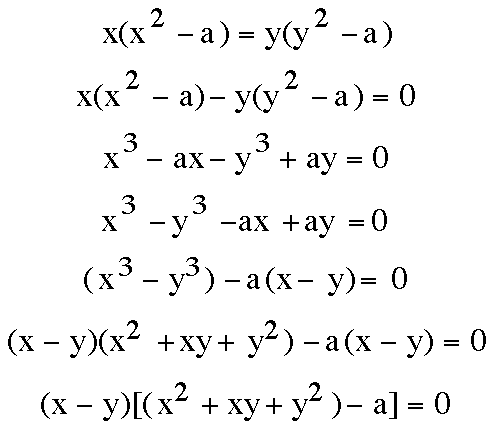
Now that we have seen what occurs to the relation equation

when a and b are greater than or equal to 1, my next investigations demonstrate the changes in the graphs that occur for other values of a and b.