Department of Mathematics Education
Dr. J. Wilson, EMAT 6690

Given any triangle ABC, construct an equilateral triangle on each side.

Find the center of each of each equilateral triangle. Recall that in equilateral triangles, the centroid, incenter, circumcenter, and orthocenter are concurrent. Therefore, we need only to construct one type of center to find all four centers. I chose to construct the perpendicular bisectors of the sides of each equilateral triangle to find the circumcenters. Constructing segments that join these three centers produces Napoleon's Triangle JKL. We will now investigate Napoleon's Triangle given an arbitrary triangle ABC.

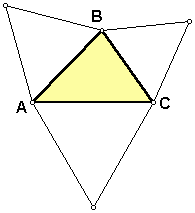
When the original triangle ABC is scalene, Napoleon's Triangle JKL is equilateral.

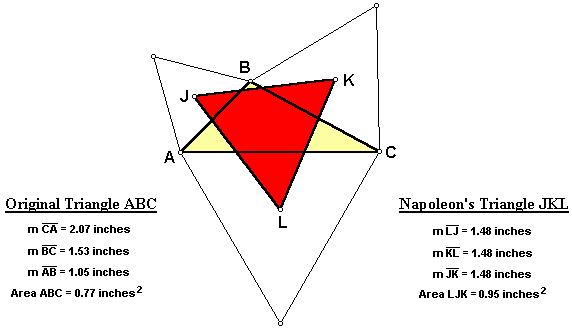
When the original triangle ABC is isosceles, Napoleon's Triangle JKL remains equilateral.

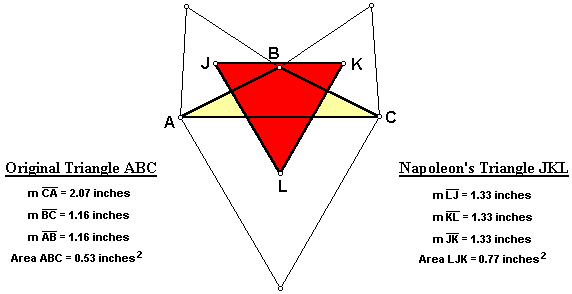
When the original triangle ABC is a right triangle, Napoleon's Triangle JKL remains equilateral.

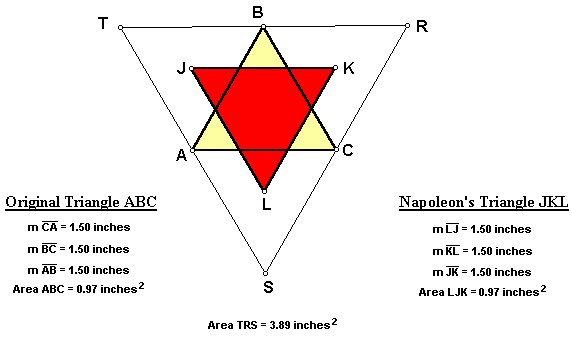
When the original triangle ABC is equilateral, Napoleon's Triangle JKL again remains equilateral. Notice that the original triangle ABC is the medial triangle of triangle RST, so triangle ABC has one fourth the area of triangle RST. Additionally, notice that the areas of the original triangle ABC and Napoleon's Triangle JKL are equivalent. Therefore, Napoleon's Triangle also has one fourth the area of triangle RST.

Through this investigation, we can conjecture that for any arbitrary triangle ABC, Napoleon's Triangle is equilateral.

Click here to investigate a GSP sketch for yourself.

The Napoleon's Triangle that we have been investigating up to this point actually is referred to as the outer Napoleon Triangle. We can construct the inner Napoleon Triangle by reflecting each center of the equilateral triangles (J, K, and L) across its corresponding edge in the original triangle ABC.

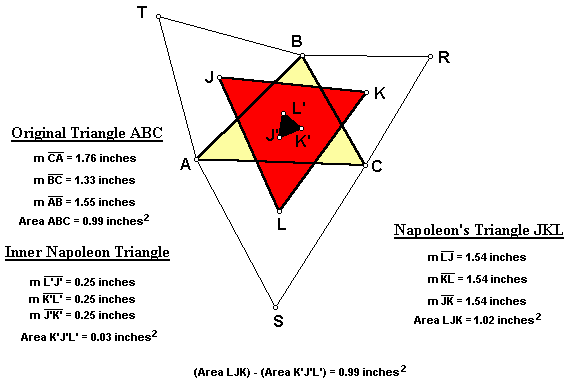
For any triangle ABC, the inner Napoleon Triangle J'K'L' is always equilateral. Additionally, the area of the outer Napoleon Triangle JKL minus the area of the inner Napoleon Triangle J'L'K' equals the area of the original triangle ABC.

Click here to investigate for yourself a GSP sketch of this conjecture.

Now construct segments connecting each vertex of the original triangle ABC with the most remote vertex of the equilateral triangle on the opposite side.

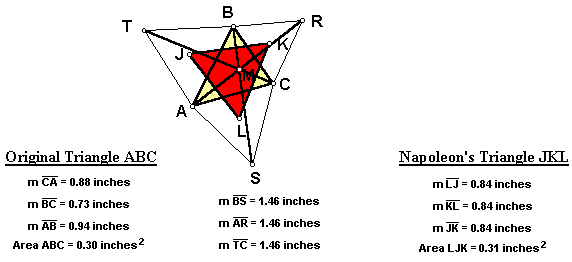
For any triangle ABC, segments AR, BS, and CT are congruent. Additionally, if segments AR, BS, and CT are constructed into lines, the three lines are concurrent at point M.

Click here to investigate for yourself a GSP sketch of this conjecture.

If you have any suggestions that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.

Return to my homepage.