Department of Mathematics Education
Dr. J. Wilson, EMAT 6690

To Prove

The bisector of an angle of a triangle divides the opposite side into segments that are proportional to the adjacent sides.

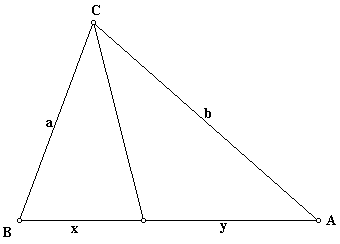
That is, for any triangle ABC, the bisector of the angle at C divides the opposite side into segments of length x and y such that

---

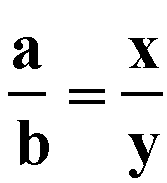
Proof

Let's construct line BE parallel to CD, intersecting line AC at point E.

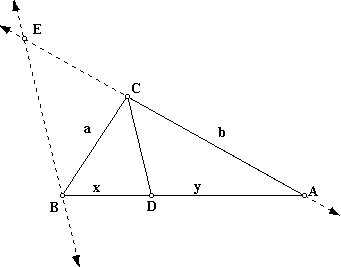
Consider triangle ABE. A line that is parallel to the third side of a triangle divides the other two sides proportionally,

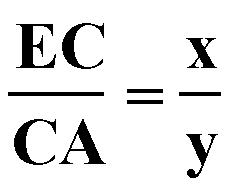
Since the relationship that we are looking for is

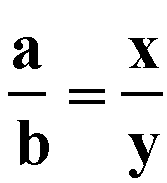
and since b is segment CA, what we need to show is that a is congruent to EC.

Consider triangle BCE. In order to show that a is to congruent to EC, we want to show that triangle BCE is an isosceles triangle.

Angle E is congruent to angle DCA because corresponding angles are congruent when parallel lines are cut by a transversal.

Let's construct a parallel line FC to BA through C.

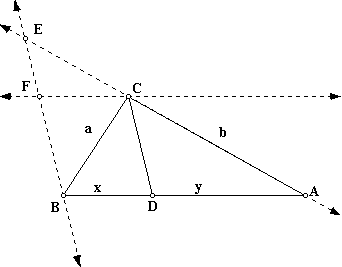
Notice that FCDB is a parallelogram. This tells us that angle FBC is congruent to angle BCD because alternate interior angles are congruent when parallel lines are cut by a transversal.

Since CD is the angle bisector of angle BCA, angle BCD is congruent to angle DCA.

Therefore, angle EBC is congruent to angle DCA by transitivity.

Recall that angle DCA is congruent to angle E. Therefore, angle EBC is congruent to angle E.

This tells us that triangle BCE is an isosceles triangle, which tells us that a is congruent to EC.

Now, our original relationship of

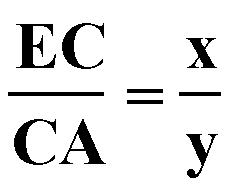
can be rewritten thrugh substitution to achieve our desired proportion

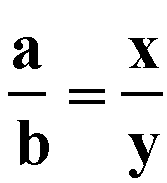
If you have any comments concerning this investigation that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.

Return to exploration page of this essay.

Return to my homepage.