

The Nine Point Circle, named for the nine constructed points on it, has several neat mathematical properties. Every triangle has a nine point circle which is connected to both it's inscribed circle, circumscribed circle, and Euler Line. It was first proven by French mathematicians Jean-Victor Poncelet and Charles Brianchon in 1821.
* Draw points A, B, and C.
* Draw intersecting straight lines from each of these points to draw a triangle.
* Construct the following segments:
* Segment m between points A and C.
* Segment n between points A and B.
* Segments o between points B and C.

* Find the midpoint on m and call it point D.
* Find the midpoint of n and call it point E.
* Find the midpoint of o and call in point F.
* Construct a perpendicular line from line m through point D and call this line p.
* Construct a perpendicular line from line n through point E and call this line q.
* Construct a perpendicular line from line o through point F and call this line r.
* Find the intersection of these lines. This point, G, is called the circumcenter.

* Hide lines p, q, and r.
* Construct a perpendicular line on o through point A. Name the perpendicular line r and label the point where o and r cross as point I.
* Construct a perpendicular line on n through point C. Name the perpendicular line s and label the point where n and s cross as point J.
* Construct a perpendicular line on m through point B. Name the perpendicular line t and label the point where m and t cross as point K.
* The lines constructed above are the altitudes of the triangle. The point of intersection, H, of the altitudes is called the orthocenter.

* Hide lines r, s, and t.
* Construct a segment between point G (the circumcenter) and point H (the orthocenter).
* Find the midpoint, N, of the this segment. This point, N, is the center of the Nine-Point Circle.
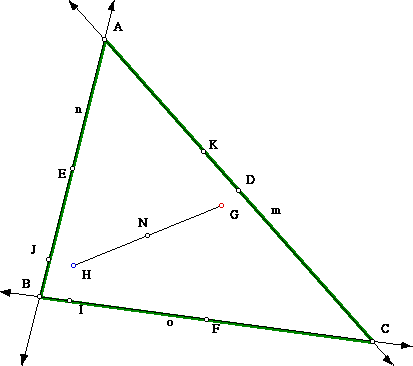
* Construct segments from H to each of the points A, B, and C.
* Construct the midpoints of each of these lines and name them P, Q, and R, respectively.

* Construct a circle with the center N, picking one of the nine points as another point on the circle.

Click here to open a GSP Sketch of the Nine Point Circle or click here to open a GSP script to see how the Nine Point Circle was constructed. Also, you may click here to see a neat GSP animation of the Nine Point Circle.