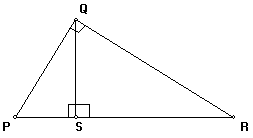
1. Use a paragraph proof to prove the similarity theorem. Use your gsp sketches and measures to help you.
We are given that 
PQR is a right angle and that segment
QS is an altitude of 
PQR. We want to show that
PSQ is similar to PQR; PQR is similar to QSR ; PSQ is similar
to QSR.
Proof:
PQR is a right angle and segment QS is an altitude,
so segment QS is perpendicular to segment RP. Thus PSQ
and RSQ are right angles by the definition of perpendicular
lines. Therefore PSQ 
PQR
and RSQ PQR
since right angles are congruent. Since congruence of angles is reflexive
we have SPQ SPQ and SRQ SRQ. Therefore by AA similarity
we have PSQ is similar to PQR; PQR is similar to QSR. Since similarity is transitive
we also have PSQ is similar to QSR.
2. Click on the GSP sketch and follow the instructions.
Then answer the following:
Using the figure to the right, name the three similar triangles
EAB is similar to AFB
EAB is similar to 
EFA
AFB is similar to 
EFA
3.
4. 
5.
6.