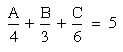
PROBLEM: A Tangled Tale
A problem from Lewis Carroll -- A man walked for 5 hours, first along a level road, then up a hill, and then he turned around and walked back to the starting point along the same path. He walks 4 mph on the level, 3 mph uphill, and 6 mph downhill. Find the distance he walked.
There is not enough information given to solve the problem.
What additional information would you need?
Usually it would matter
what portion of the walk was on level ground and what portion
was on the slope. Why does
it not matter in this case?
Find the average rate for
the uphill and downhill portions of the walk. Remember, the average
rate is over the same
distance each way, and the average rate is NOT the arithmetic
mean of the two rates. That is, the rate is NOT 4.5
mph.
Hint?
Find the average rate for
the uphill and downhill parts of the walk.
Solution: The man walked twenty (20) miles in five hours. In order for my students to grasp how far he has walked, it might be sufficient to go outside and actually get involved with this. The kids will appreciate the outdoors for that particular day and they will get tired from the 20 miles of walking...although I really doubt I would make them that far...maybe one quarter of the total distance and they can figure out how much farther they would have to travel. Here is how you find the answer:
I will let A be the distance the man walked on level ground. I will let B equal the distance that he travels uphill, and C equal the distance he travels downhill. Therefore, A = 4 mph, B = 3 mph, and C = 6 mph. Since it is given that he walks a total of 5 hours, I set up the following proportional equation:
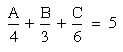
Right here I would remind my students to take another look at the problem at hand. I would ask them what does it ask. I would point out that the man is still traveling the same distance uphill as he is going downhill, therefore the problem should look like this:
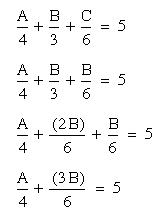
I guess I want to know where I go from here. Looking at the problem, I see that I have two unknowns. Because I have looked at Dr. Wilson's answer, I have realized that I must get to my solution of 20 miles.
Here is where I probe my students to get into groups of three or four, discuss, probe, ask a million questions, draw out their ideas, and/or even come up with a neat game or some sort of strategy to answer the question.
If they cannot come up with a solution, I would tell them that a wise man once told me to seek and ye shall find. So, I did do this myself. I have included some work of other students from Dr. Wilson's previous classes. See what they did...then ask the students how did they come up with their answers.
Sandra McAdams, Susan Pinion, & Lisa Stueve
Angie Head, Beth Richichi, & Teisha Wright