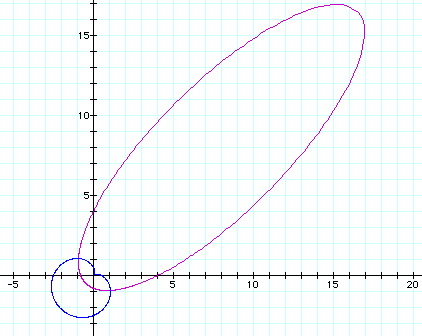Consider the following equation in polar form ![]() .
Graphing the equation using software is an easy matter. When we
do so the resulting graph is an ellipse centered at the point
(3,0).
.
Graphing the equation using software is an easy matter. When we
do so the resulting graph is an ellipse centered at the point
(3,0).
.gif)
To verify that this is an ellipse centered at (3,0) we can convert the equation from polar to rectangular form using the following conversion formulas
![]() ,
,
![]() ,
, ![]()
.
Cross multiplying results in the equation ![]() ,
into which one can substitue for r and
,
into which one can substitue for r and ![]() resulting
in the equation
resulting
in the equation ![]() .
Now simpify this equation so that the final form is
.
Now simpify this equation so that the final form is ![]() ,
where (h,k) is the center of the ellipse.
,
where (h,k) is the center of the ellipse.
Your equation should be![]() .
It is clear that this is the correct equation since the major
axis has length 5 units and the minor axis has length two units.
.
It is clear that this is the correct equation since the major
axis has length 5 units and the minor axis has length two units.
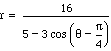
Graphing the polar equation above using a graphing utility
one can see that the ellipse has the same size and shape it is
simply tilted so that the major axis now lies along the line ![]() .
.

One might conclude that subtracting ![]() inside
the arguement produced this tilt. To investigate this hypothesis
simply graph the equation using a range of radian values subtracted
inside the arguement.
inside
the arguement produced this tilt. To investigate this hypothesis
simply graph the equation using a range of radian values subtracted
inside the arguement.
The red ellipse graphed below is 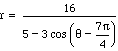 ,
the purple ellipse is
,
the purple ellipse is  ,
and the blue ellipse is
,
and the blue ellipse is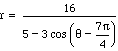 .
.

And we can see by graphing the major axes of each of the ellipses
above that indeed the ellipse with an arguement of theta minus
x radians has a major axis of ![]() .
.

We can generate hyperbolas using equations in polar form similar to the one below.

It is interesting to graph the denominator of the equation in polar coordinates on the same axes as the numerator.
The blue cardiod is generated by the polar equation![]() in the denominator and the purple hyperbola is generated by the
entire equation.
in the denominator and the purple hyperbola is generated by the
entire equation.
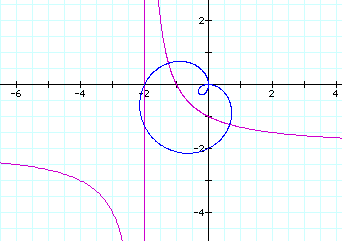
So now how does a hyperbola result? As theta approaches some value the denominator of the polar equation must approach zero. What values of theta could produce this effect?
Set ![]() equal
to zero and solve for theta. This process generates four values
of theta that generate radi of zero. One can almost guess what
they are from looking at the graph of the cardiod (0, pi, pi/2,
3pi/2).
equal
to zero and solve for theta. This process generates four values
of theta that generate radi of zero. One can almost guess what
they are from looking at the graph of the cardiod (0, pi, pi/2,
3pi/2).
But generating a hyperbola is contingent on being able to get
zero in the denominator of the equation, hence if the equation
was written ![]() the
only values of x that generate hyperbolas are on the interval
between negative square root of two and square root of two. If
x is greater than square root of two one will generate an ellipse.
Try some examples. The case with x = 1.5 is generated below.
the
only values of x that generate hyperbolas are on the interval
between negative square root of two and square root of two. If
x is greater than square root of two one will generate an ellipse.
Try some examples. The case with x = 1.5 is generated below.
![]()