Stephanie K. Lewis

Assignment 7

EMAT 6680

Fall '98

Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.

The red circle represents the constructed circle that is tangent to both the small and large black circles.

As I observed the example that was given in the Assignment 7 guidelines, and compared it to my own construction, I noticed that the circle I constructed (red circle) was on the outside of the original small black circle. The constructed tangent circle in our guideline illustration was not on the inside of the constructed circle, but on the outside. However, I imagine that this does not matter since the constructed red circle is indeed tangent to both the original black circles.

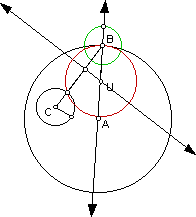
With further investigation, I found that the if the vertex of the isosceles triangle was at the center of circle B, then the constructed tangent circle U would not enclose circle C. However, if the vertex of the isosceles triangle was at the intersection of a point on circle B and the diameter of Circle A, then the constructed tangent circle would enclose circle C. In either case, the constructed red circle is tangent the given circles C and circle A.

*A7,A71.gsp,A702.gsp