

I chose problem 2 from assignment 1 for this write-up:
"2. Make up linear functions f(x) and g(x). Explore, with diffefent pairs of f(x) and g(x) the graphs for
i. h(x) = f(x) + g(x)
ii. h(x) = f(x).g(x)
iii. h(x) = f(x)/g(x)
iv. h(x) = f(g(x))
Summarize and illustrate."
I utilized the Algebra Xpresser and Graphing Calculator software during my investigation.
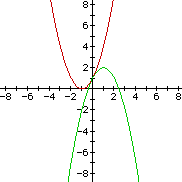
First, I chose two linear functions for f(x) and g(x). I used y=2x+3 for f(x) and
y=x+1 for g(x).
The graph of f(x) [red] and g(x) [green] are shown:

The sum of f(x) and g(x): f(x) + g(x) = (2x+3) + (x+1) = 3x+4.
This is still in the form of equation for a line. So I would expect the graph to be linear.
The graph of the sum of f(x) and g(x) [red] is shown:
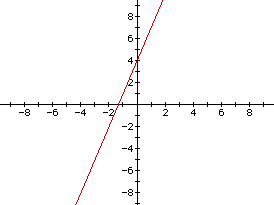
This is a linear function as expected The sum of two linear functions is true for this example. Is it true for all linear functions? Let f(x) be y=-2 and g(x) be y=5.
The graph of f(x) [red] and g(x) [green] is shown:
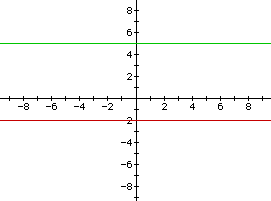
The sum of f(x) and g(x) is f(x)+g(x)=-2+5=3.
The graph of f(x)+g(x) is shown:

What if both functions are vertical lines? Let f(y) be x=1 and g(y) be x=3. Then the sum of f(y) and g(y) would be: f(y)+g(y)=1+3=4.
The graphs f(y) [red], g(y) [green], and f(y)+g(y) [blue] are shown:
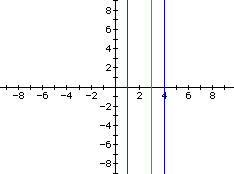
So far, the sum of two linear functions is a linear funciton. Is it always true that if f(x) and g(x) are linear functions, then f(x)+g(x) is a linear function?
Suppose f(x)=mx+b and g(x)=nx+c for real numbers x,m,b,n, and c.
Then f(x)+g(x)=mx+b+nx+c=(m+n)x+(b+c). But this is still in the form of a linear function.
Now, look at the product of the original f(x) and g(x) where y=2x+3 is f(x) and y=x+1 is g(x).
f(x)g(x)=(2x+3)(x+1). Expand the terms to get the quadratic equation:
![]() . Now we suspect that the
graph will be a parabola. Let's solve for the x-intercepts. 0=(2x+3)(x+1),
so the x-intercepts will be at x=-1 and x=-1.5. The y-intercept
will be (at x=0): y=3.
. Now we suspect that the
graph will be a parabola. Let's solve for the x-intercepts. 0=(2x+3)(x+1),
so the x-intercepts will be at x=-1 and x=-1.5. The y-intercept
will be (at x=0): y=3.
The graph of f(x)g(x) is shown:

This parabola opens upward.
Now, look at the product of f(x) and g(x) when f(x)=-2 and g(x)=5. The product f(x)g(x)=-10. The resulting graph is a horizontal line at y=-10. This graph is not shown.
Now, look at the product of f(y) and g(y) when f(y)=1 and g(y)=3. The product f(y)g(y)=3. The resulting graph is a vertical line at x=3. This graph is not shown.
Now, look at the product f(x)g(x) when f(x)=-2x+3 and g(x)=x+1. Then the product f(x)g(x)=(-2x+3)(x+1). Expand the terms to get the quadratic equation:
![]() .
.
Again, the graph should be a parabola. Solve for the x-intercepts. 0=(-2x+3)(x+1). So, the x-intercepts are at x=1.5 and x=-1. The y-intercept will be (at x=0): y=3. The graph is shown:
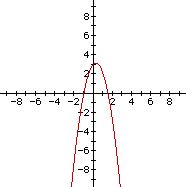
Notice this parabola opens downward. Is the reason for the downward opening due to the coefficient of the x-squared term, the x term, or the constant 3? It is not the constant 3, because the parabola before this one above opens up and has the same constant of 3 in the equation. Most everyone will remember from high school that it is the coefficient of the x-squared term being negative that causes the parabola to open downward. To prove this graphically, let's graph the following equations:
The only difference is the coefficient of the x-squared term. So, when the coefficient of the x-squared term is negative, the parabola opens downward. Also notice that both parabolas have a y-intercept of 1. This is related to the constant "1" in each equation. When the equation for the parabola is in the form:
the constant "c" is the y-intercept. Look at the following graphs:
The only difference in these equations is the constant term. The y-intercept is determined by the constant "c".
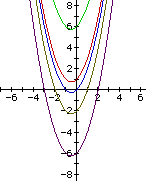
Now look at the following products of linear equations:

The product of two linear functions in all of the above cases results in a parabola. Now look at the following product of two linear functions: y=0x+3 [red] and y=x+3 [green].

This results in a line. The reason is because the x-squared term has zero for the coefficent. Now look at the following two parabolas:

Notice that as the coefficient of the x-squared term becomes small, the parabola starts to unfold to become a line. As the coefficient of the x-squared term becomes large, the parabola collapses to become a ray. These two particular parabolas are the following products of linear functions:
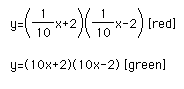 .
.So, in every case, the product of two linear functions has resulted in a parabola. There is one occasion when the parabola is degenerate (x-squared coefficient = 0, parabola unfolds to become a line). When the x-squared coefficient gets infinitely large (positive or negative), the parabola appears to collapse to become a ray; however, one could argue that is still a parabola with two sides that are inifinitely close together.
Now let's look at ratios of the following linear functions:
f(x)=x-3; g(x)=x+3; h(x)=-x-3; j(x)=-x+3; k(x)=10x-2; m(x)=0x+2; n(x)=x; p(x)=-x.
First, the ratio of f(x)/g(x):
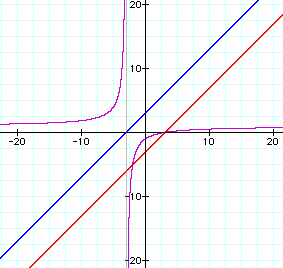
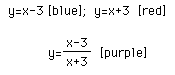
The result is a hyperbola. So let's look at the ratio of f(x)/h(x):
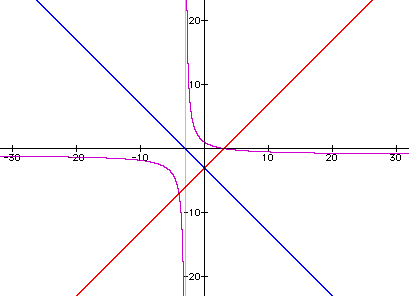
Again the ratio of two linear functions is a hyperbola. Now, let's look at the ratio of k(x)/p(x):
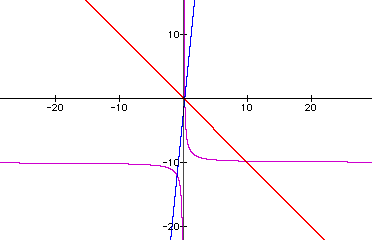
Once again a hyperbola results from the ratio of two linear functions. Notice that the vertical asymptote for each of these ratios occurs for the value of x that makes the denominator = 0. Notice that the horizontal asymptote occurs at the value of y corresponding to the ratio of the coefficients of the x-term.
O.K. Let's look at the ratio of k(x)/m(x):
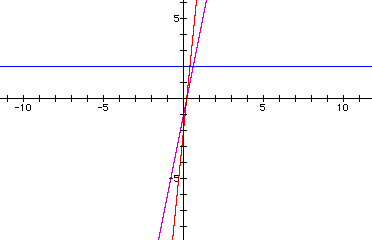
Now the result is a linear function. Specifically, the ratio is the linear function y=5x-1. What about the ratio of m(x)/k(x):
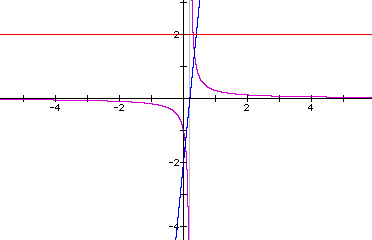
A hyperbola again. The vertical asymptote occurs at x=1/5, i.e. when the denominator = 0. The horizontal asymptote occurs at y=0, i.e. the ratio of the coefficients of the x-terms.
Let's look at the ratios of n(x)/p(x) and f(x)/f(x):
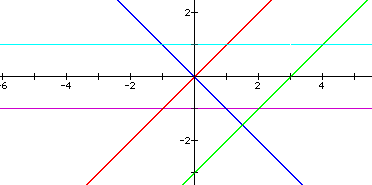
These both results in linear functions. This is because the ratios were -1 and 1 respectively.
Let's look at h(x)/j(x):
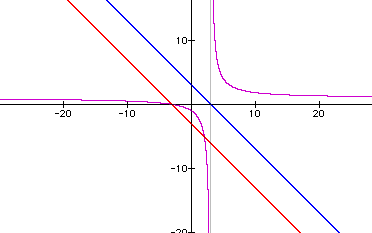
Hyperbola again. Vertical and horizontal asymptotes hold the same pattern as before.
Let's look at the ratio of f(x)/k(x):
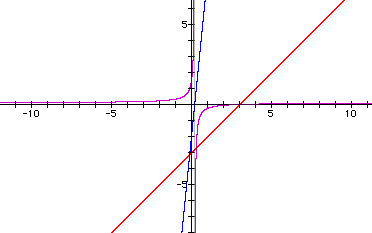
Hyperbola with vertical and horizontal asymptotes following the same pattern. However, notice this is only the second time that the hyperbola opens toward the 2nd and 4th quadrants. All of the others have opened toward the 1st and 3rd quadrants. Why? Is there a pattern?
Let's look at the ratio of k(x)/f(x)

This time the hyperbola opens toward the 1st and 3rd quadrants instead of the 2nd and 4th as was the case in the ratio for f(x)/k(x). Does this happen everytime that we look at the reciprocal of a ratio?
Let's look at a few to find out:
First, j(x)/h(x) (red) and h(x)/j(x) (blue):
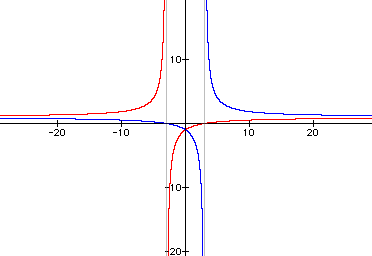
It happened here.
Next, p(x)/k(x) (red) and k(x)/p(x) (blue):

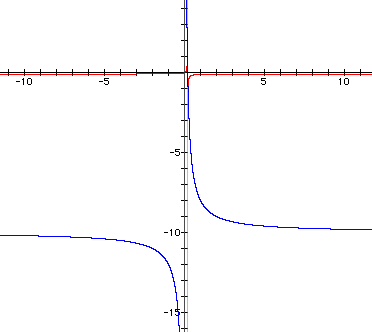
It happened this time also.
Next, let's look at k(x)/m(x) (red) and m(x)/k(x) (blue):

Remember that k(x)/m(x) was a linear function (or some might say degenerate hyperbola).
Let's look at (2x+5)/(x-2) (red) and (x-2)/2x+5) (blue):

Same patterns hold true here also.
Let's look at (2x+1)/(x-2) (red) and (x-2)/(2x+1) (blue):

Let's look at (2x-1)/(x+2) (red) and (x+2)/(2x-1) (blue):
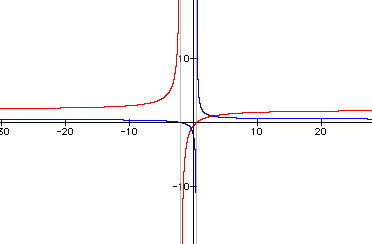
O.K. Now the direction that the hyperbola open swithes. It appears that both hyperbola have been reflected about the y-axis.
Let's look at -(2x-1)/(x+2) (red) and -(x+2)/(2x-1) (blue):
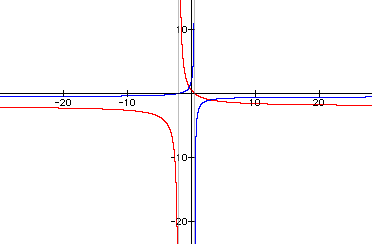
This appears to have changed the orientation of the two parabolas. In fact both hyperbola have been reflected about the x-axis as was expected.
I still have not recognized a pattern to determine the initial orientation of the parabola for a ratio of linear functions, but have noticed that the reciprocal ratio will switch the orientation of the parabola. However, the asymptotes are easy to determine for a ratio of linear functions.
Now let's look at the compostion of the following linear functions:
f(x)=x-3; g(x)=x+3; h(x)=-x-3; j(x)=-x+3; k(x)=10x-2; m(x)=0x+2; n(x)=x; p(x)=-x.
First, the compositon of f(g(x)):
f(g(x)) = (x+3)-3 = x. This is still is linear function.
Let's look at some more compositions:
k(m(x)) = 10(0x+2)-2 = 0x+20-2=18. This is a linear function.
p(n(x))=-(x)=-x, a linear function.
g(k(x))=(10x-2)+3=10x-2+3=10x+1, a linear function.
It appears that a composition of linear functions will always be a linear function.
Let's look at the general equation for a line in a composition with itself.
Let q(x)=mx+b. So q(q(x))=m(mx+b)+b=m^2x+mb+b=nx+c, where n=m^2 and c=mb+b.
So q(q(x))=nx+c which is a linear function.
A composition of linear functions will be a linear function.
Summary:
The sum of two linear functions is a linear function.
The product of two linear functions is a parabolic function with a special case when atleast one of the linear functions is a horizontal line. This special case results in a linear function or some would say a degenerate parabola.
The quotient (or ratio) of two linear functions is an hyperbolic function with a special case when the linear function in the denominator is a horizontal line. This special case results in a linear function or some would say a degenerate hyperbola.
The composition of two linear functions is a linear function.