

Problem:
Investigate (vary a, b, and k):
r = a + b cos(kt) and r = a + b sin(kt).
Limacons ("Lee-ma-sahn") have the form:
r = a + b cos(t) and r = a + b sin(t), where a,b are nonzero real numbers.
Let's look at r = 1 + cos(t)(blue) and r = 1 + sin(t) (magenta):
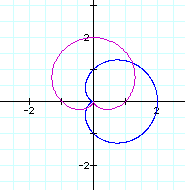
These are commonly called cardioids. They are one type of Limacon.
Notice that r = 1 + cos(t) is a 90 degree rotation of r = 1 + sin(t).
What does r = 1 - cos(t) look like?

This is simply a reflection about the y-axis. This was expected since we graphed r = a + -f(t) ; instead of r = a + f(t).
Click here to see a movie of r = 1 + cos(t) and r = 1 + sin(t).
Let's look at r = 0.5 + cos(t) (blue), r = 0.5 + 0.5 cos(t) (magenta), and 2 + cos(t) (red):
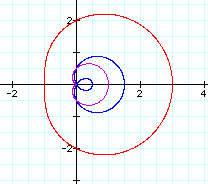
Notice that the magenta curve is a cardioid (in fact it is 0.5(1 + cos(t))).
But the blue curve is different. This is sometimes referred to as a limacon with an inner loop.
The red curve is different also. It appears to flatten on one side. Sometimes this is considered a convex limacon.
Let's look what happens when we make "a" larger or smaller for r = a + b cos(t):
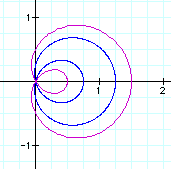
As "a" gets larger, the outer loop gets larger and the inner loops becomes smaller. The reverse is true as "a" gets smaller.
Let's look at r = 1.5 + cos(t):
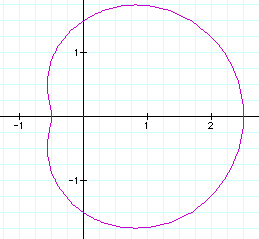
This is a dimpled limacon.
Now,
what happens as "k" is varied:
We'll start with k = 0; a = 0.25, b = 1, c 1.5:
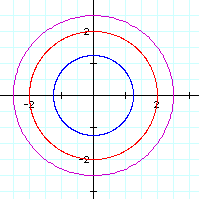
Now, let's look at k = 1; a = 0.25, b = 1, c 1.5:

Now, let's look at k = 2; a = 0.25, b = 1, c 1.5:

Now, let's look at k = 3; a = 0.25, b = 1, c 1.5:

Now, let's look at k = 4; a = 0.25, b = 1, c 1.5:

Now, let's look at k = 5; a = 0.25, b = 1, c 1.5:

Any conjectures? Is there anything similar to what happens as "k" is varied for the curve r = cos(kt) or r = sin(kt)?
Try graphing them and see what happens.
Click here to see a movie of these graphs.
Return to Chris McCord's EMAT 6680 Assignment Index Page
Return to Chris McCord's EMAT 6680 Homepage