

Problem:
1. Construct a triangle and its medians. Construct a second
triangle with the three sides having the lengths of the three
medians
from your first triangle. Find some relationship between the two
triangles. (E.g., are they congruent? similar? have same area?
same perimeter? ratio of areas? ratio or perimeters?) Prove whatever
you find.
3.
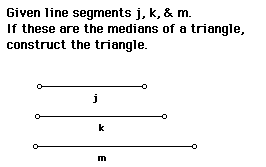
Problem 1:
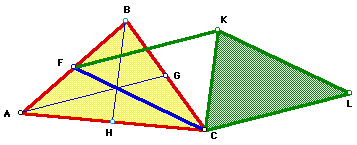
Given triangle ABC.
Segments AG, BH, and CF are the medians for triangle ABC.
Segment FK is parallel to segment AG. Segment CL is parallel
to FK, thus it is parallel to segment AG.
Segment CK is parallel to segment BH.
Segment KL is parallel t segment FC.
Triangle CFK was constructed using the lengths of the medians
for triangle ABC. Triangle CKL was constructed by reflecting triangle
CFK about the line CK. So triangle CKL has sides consisting of
the lengths of the medians of triangle ABC. Also, triangle CFK
and triangle CKL are congruent triangles.
If you want to investigate the relationship between triangle ABC and triangle CKL, click HERE.
After some initial investigations, a relationship between the areas of the triangles was uncovered. The relationship appears to be that the area of triangle CKL is 3/4 of the area of triangle ABC.
Can this be proven? (Yes, and I'll try.)
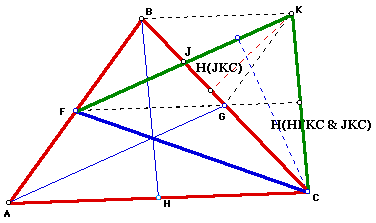
The original triangle is triangle ABC. In order to proved that area of triangle CKL is 3/4 the area of triangle ABC, it will suffice to show that the area of triangle FKC is 3/4 the area of triangle ABC.
BKCH is a parrellelogram. Thus triangle BKC and triangle BCH have congruent areas.
The area of triangle BKC = 1/2 * (BC * H(JKC)). H(JKC) is the dashed red line from point K to segment BC.
The area of triangle JKC = 1/2 * (JC * H(JKC)). H(JKC) is the dashed red line from point K to segment BC.
Note that the area of triangle ABC is twice the area of triangle BCH. (Each triangle has the same altitude and AC = 2 * HC) Since triangle BCH and triangle BKC have congruent areas, then the area of triangle ABC is twice the ares of triangle BKC.
So the area of triangle ABC = 2 * (1/2 * (BC * H(JKC))) = BC * H(JKC).
Similarly, the triangle FKC has twice the area of triangle JKC (Each has the same altitude shown by dashed blue line and FK = 2 * JK). FK = 2 * JK because segment BG bisects segment FK since they are diagonals of the parrellelogram FBKG.
Also, segment FK bisects BG for the same reason. Since G is the midpint of BC, it follows that JC = 3/4 BC.
Thus, the area of triangle JKC = 1/2 * (3/4 * BC * H(JKC)).
So the area of triangle FKC = 2 * [1/2 * (3/4 * BC * H(JKC))] = 3/4 * BC * H(JKC).
Thus the area of triangle FKC = 3/4 area of triangle ABC.
Thus the area of triangle CKL is 3/4 the area of triangle ABC.
Other relationships noticed: when triangle ABC is an equilateral triangle, triangles ABC and CKL are similar triangles. The ratio of the perimeter of triangle CKL to the perimeter of trianle ABC varied between 0.72 and 0.99. I suspect that the ratio of the perimeters can be reduced to less than 0.72.

Click here to construct a triangle given the lengths of its medians.
Click here to construct a triangle given a triangle constructed from the lengths of its medians.
Click here to see the construction of a triangle given the lengths of its medians. You will have to open a GSP sketch and construct the three medians (i.e. three segments) and highlight (select) the endpoints before running the script.