

Let triangle ABC be any triangle and let point P be any point in the plane. Construct the lines through point P perpendicular to the sides (extended if necessary) of triangle ABC. The points R, S, and T constructed by the intersection between the sides of triangle ABC and the perpendicular lines through point P form the vertices of the pedal triangle for the pedal point P.

Click here to investigate the Pedal Triangle as the Pedal Point P moves (You must have GSP on your computer to conduct this investigation.)
What happens when the Pedal
Point is on triangle ABC?
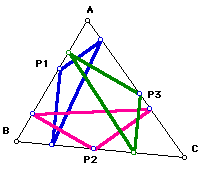
The blue triangle is the pedal triangle for the point P1 on segment AB.
The pink triangle is the pedal triangle for the point P2 on segment BC.
The green triangle is the pedal triangle for the point P3 on segment AC.
Is the pedal point always a vertex of the pedal triangle when the pedal point is on a side of triangle ABC? Click here for answer.
Click here for GSP animation.
What happens when
Point P is on the circumcirlce?

It appears that the points R, S, and T are collinear. Is it always the case?
Click here to investigate the pedal point as a point on the circumcircle.
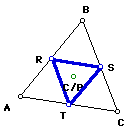
The pedal triangle appears to be the medial triangle. Is it? Click here to investigate.
Return to Chris McCord's EMAT 6680/Home Page
Return to Chris
McCord's EMAT 6680 Assignment Index Page